「データを使って将来を予測したい」と考えたとき、避けて通れないのが**「定常性(ていじょうせい)」**という言葉です。
統計学や時系列分析の本を開くと必ず出てくる用語ですが、数式ばかりで挫折した方も多いのではないでしょうか?実は、定常性は**「そのデータは、未来を予測できる状態にあるか?」**を判断する、非常にシンプルな基準なのです。
今回は、定常性の意味と、なぜそれが分析に不可欠なのかを、図解とともに解説します。数式や定義で理解しようとすると大変ですが、グラフで見れば一目瞭然です。
1. 定常性とは「データのルールが変わらないこと」
一言で言うと、定常性とは**「時間に関係なく、データの統計的な性質が一定である状態」**を指します。
もっと直感的に言えば、**「データのどこを見ても性質が同じ」**ということです。
定常なデータが満たす3つの条件
専門的には以下の3つのルールが守られている状態を「(弱)定常性」と呼びます。
定常なデータのデータは以下の特徴を持ちます。
- 平均が一定: グラフがずっと右肩上がりだったりせず、ある一定の数値(平均値)の周りをウロウロしている。
- 分散(ばらつき)が一定: データの振れ幅が途中で変わらない。
- 自己相関が一定: 「昨日の値が今日にどう影響するか」というルールが、どの時点でも同じ。
定常なデータをグラフにすると以下のようになります。平均値はおおむね一定のままで、データのばらつきの範囲も急激に広がったりすることはありません。
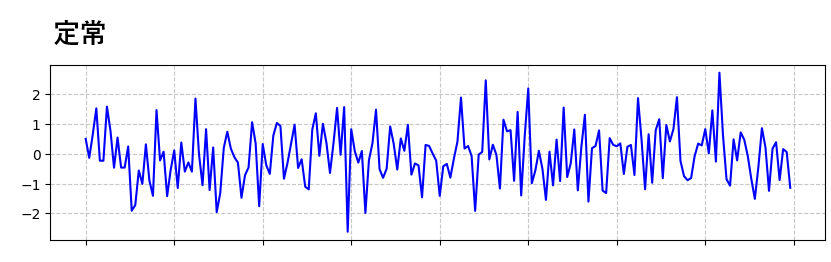
非定常なデータってどんなもの?
では、定常ではないデータというのはどんなものでしょう?
ここから先はそのようなデータをグラフで視覚的に確認していきましょう。
以下に挙げるようなデータは非定常データと呼ばれ、ARIMAモデル系の方法ではすぐに解析することが出来ません。
平均が一定ではない
例えば「平均が一定でないグラフ」はこんなものです。どちらも、データが徐々に上がったり下がったりしており、見る場所によって平均値が変わってしまいます。このようなデータは非定常であるとされます。
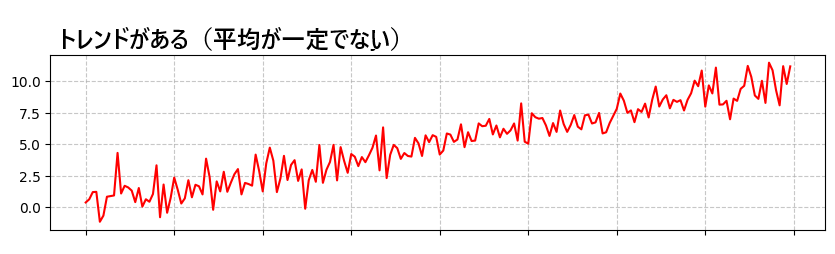
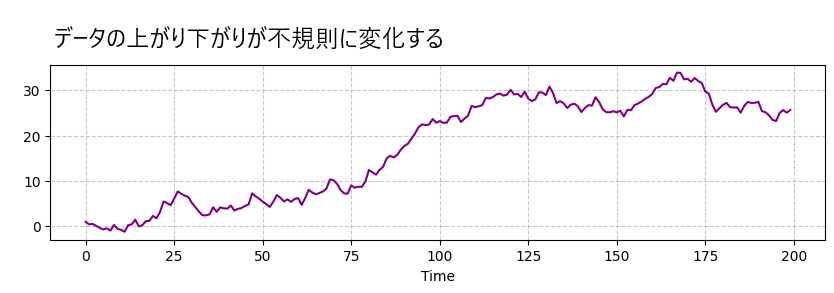
分散が一定ではない
「分散が一定でないグラフ」は以下のようなものです。後半に行くにつれ徐々にデータのばらつきが大きくなっているのがわかります。このようなデータも非定常であるとされます。
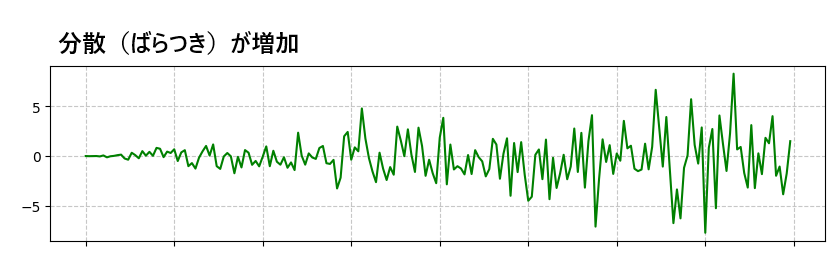
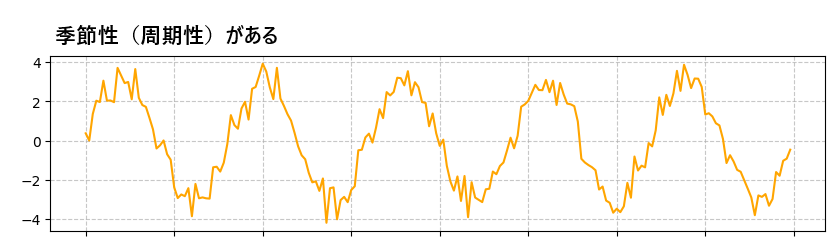
季節性がある
「季節性のあるグラフ」は以下のようなものです。周期的にデータが変動しているのがわかります。このようなデータも非定常であるとされます。
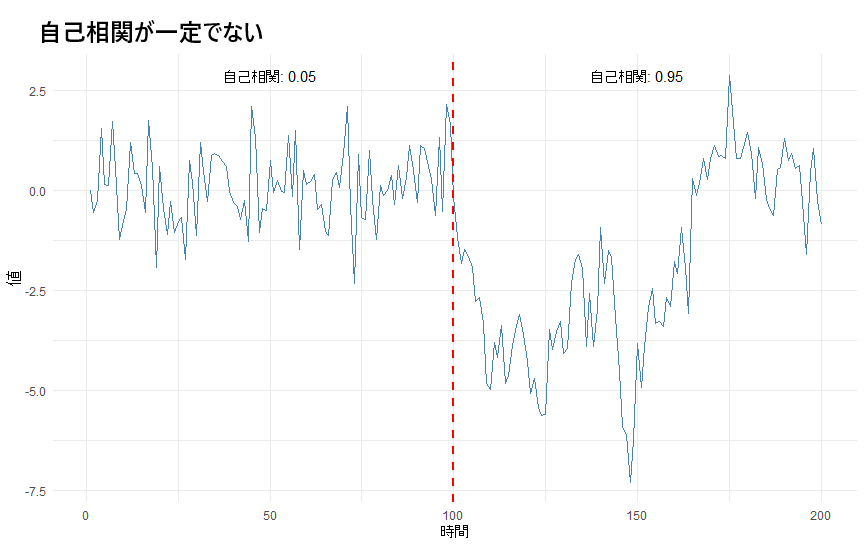
自己相関が一定ではない
「自己相関が一定でないグラフ」は以下のものです。「自己相関」はややわかりにくい概念ですが、「昨日調子が良かったので今日も調子がいい」といったように前の段階の影響をどの程度受けるか?の程度を表すものです。下のグラフでは、左半分は前の段階の影響をほとんど受けず、右半分は影響を強く受けるようになっています。途中からデータの挙動が変わっているのがわかります。このようなデータも非定常であるとされます。
2. なぜ「定常性」が重要なのか?
なぜ、わざわざ定常性にこだわるのでしょうか?それは、**「ルールがコロコロ変わるデータの未来は予測できないから」**です。
予測の前提が崩れる
私たちが過去のデータから未来を予測できるのは、「過去に起きたパターンは、将来も繰り返されるだろう」という前提があるからです。
もしデータが「非定常(ルールが常に変化する)」だと、過去にどんなに精度が高いモデルを作っても、未来予測では全く役に立たないという現象が起きてしまいます。
多くの分析手法は「定常」が前提
統計分析でよく使われるARIMAモデルは、データが定常であることを前提に設計されています。つまり、定常性を確認することは、分析のスタートラインに立つための最低条件なのです。
3. 現実のデータは「非定常」だらけ
残念ながら、私たちが扱うデータのほとんどは「非定常」です。
- ビジネス: 株価や売上(長期的なトレンドがある)。
- 医療・気象: インフルエンザの流行やアイスの売上(季節性がある)。
これらは時間によってルールが変わるため、そのままでは分析に使えません。
どうやって解決する?
そこで、非定常なデータを加工して「定常」に変える工夫をします。
たとえば徐々にばらつきが増えながら平均値も増加していくようなデータであれば、以下のような処理を行います。
1、対数変換してデータのばらつきを整える。
2,データの差分をとり平均値を一定にする。
文字で見るとわかりづらいため、グラフで見てみましょう。

4. 定常性を確認するステップ
実際に分析を進める際は、以下のステップを踏むのが一般的です。
- 可視化する(目視): まずは折れ線グラフを描き、「右肩上がりになっていないか?」「ある時期だけガタガタしていないか?」などをチェックします。
- 統計的検定(ADF検定など): 目視だけでは主観が入るため、「このデータは定常と言い切れるか?」を数学的にテストします。健康診断の数値チェックのようなものです。
まとめ:定常性は「分析のパスポート」
定常時系列分析における定常性とは、一言でいえば**「データのルールが時間によって変わらないこと」**です。
定常性のポイント
- 3つの条件: 「平均」「分散(ばらつき)」「自己相関」がずっと一定であること。
- なぜ重要か: 過去のルールが未来も続くからこそ、私たちは予測ができる。ルールが変わる(非定常な)データでは、予測の信頼性が失われてしまう。
- 非定常への対策: 現実のデータ(株価や売上など)は非定常なものばかり。そのため、**「対数変換」や「差分」**といった加工を施して、定常な状態へ整えてから分析するのが鉄則。
分析を進める2ステップ
- 目視(グラフ): まずはグラフを描き、今回紹介した「4つの非定常パターン」に当てはまっていないか確認する。
- 検定(ADF検定など): 数学的なテストを行い、客観的に定常性を判断する。
「このデータは、未来を予測できる状態にあるか?」 分析を始める前に、まずはグラフを描いてこの問いを自分に投げかけてみてください。定常性を意識するだけで、あなたのデータ分析の精度はぐっと高まるはずです。



コメント