前回の記事では、「時系列分析とはなにか？」についてお話ししました。今回は、最も基礎的な予測モデルのひとつである ARMAモデル について、なるべくやさしく紹介していきます。
医療や介護の現場でも、「予測」が役に立つ場面はたくさんあります。たとえば、こんなことを考えることはありませんか？
- 来月の入院患者数はどれくらい？
- 今月、感染防止に使う消耗品はどれくらい使いそう？
- 整形外科の入院が冬に増えるっていうけど、どのくらいの増え方？
こんなふうに、「これからどうなりそうか？」をデータから読み解く力が、時系列分析にはあります。
ARMAモデルってなに？
ARMAモデルという名前、いきなりちょっととっつきにくいですが、もとにしている発想は意外とシンプルです。
AR：自己回帰（Autoregressive）
これは、ざっくり言うと「今のデータは、直前のデータと似ているはず」という考え方です。
たとえば、毎日記録している外来患者数のようなデータでは、「昨日と今日で、そんなに大きくは変わらないよね」という感覚に近いです。
つまり、「今日の値 ≒ 昨日の値 × 係数 ＋ 誤差」というような形で予測するのが、ARモデルの基本的な考え方です。
誤差のことは考えずに、シンプルなモデルで予測をしてみると以下のような関係になります。
MA：移動平均（Moving Average）
こちらはちょっと変わった発想です。
「昨日の予測が外れたなら、今日の予測も同じように外れるかも」というように、過去の“予測の外れ具合（誤差）”から今の値を予測するという方法です。
こちらもシンプルなモデルで予測をしてみると以下のような関係になります。
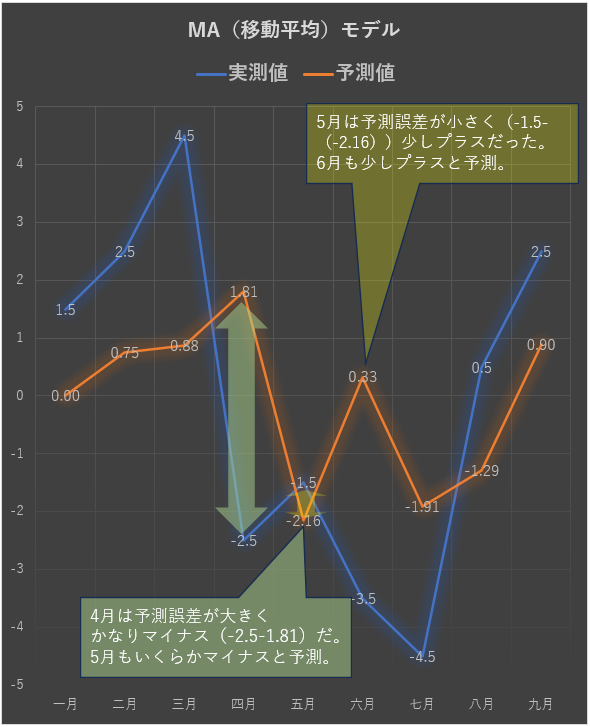
AR + MA = ARMAモデル
この AR（過去の値） と MA（過去の誤差） の両方を組み合わせたものが、ARMAモデル（自己回帰移動平均モデル）です。
🧠 イメージすると、
- ARは「患者さんは昨日のような状態だろう」
- MAは「昨日の読み間違い分を、今日に反映して調整しよう」
という感じです。
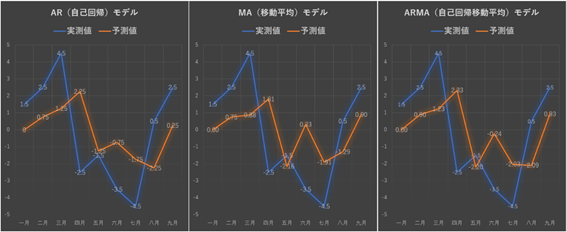
同じデータをもとに、三つのモデルでの予測を並べると下のグラフのような感じになります。
オレンジの予測値は大体似たような動きですが、5月や6月は少し差が出ていますね。
ARMAモデルを使うときの注意点：定常性
ARMAモデルを使うには、ひとつ大きな前提条件があります。
それは、「定常（ていじょう）なデータであること」。
定常データって？
ざっくり言うと、「時間が経っても、平均やばらつきが変わらないデータ」のことです。
たとえば、
- 毎日だいたい50人前後が外来に来る病院（平均が安定）
- 月ごとに患者数の波はあるけど、それが毎年同じリズムで繰り返されている（ばらつきが一定）
こういったデータは「定常的」だと言えます。
逆に、
- 毎月どんどん患者数が増えていっている（上昇トレンドがある）
- 毎年冬に入院患者数が増える（周期性がある）
といった場合は「非定常データ」になります。
このような場合はひと工夫が必要で、SARIMAモデルのような別のモデルを使う必要があります。
このあたりについては、次回の記事で紹介していきます！
おわりに：ARMAは“はじめの一歩”
ARMAモデルは、時系列分析の中でも、さまざまな発展型モデルの基礎となるモデルです。
SARIMAモデル や SARIMAXモデル は、ARMAモデルをベースに、データの持続的な増減（トレンド）や周期性に対応した“進化版”です。
次の記事では、そんなARMAの進化形であるSARIMAXモデルについて、もう少し詳しく紹介していきます！
📌 まとめ
- ARMAモデルは、過去の値（AR）と過去の予測ミス（MA）を使って未来を予測するモデル。
- 「定常性」があるデータにしか使えないので、非定常な場合は前処理や別のモデル（例：SARIMA）が必要。
コメント