多重比較とは？多重比較の種類・論文への書き方までTukey法・holm法など主要6種をスッキリ整理！

はじめに
多重比較とは何か？
有意水準5%の本当の意味
t検定を繰り返すと何が起こるのか？
「多重比較問題」と「多重比較法」を区別しよう
「ANOVAをやっていれば安心」ではない
ノンパラメトリック検定でも必要？
代表的な多重比較法（事後検定）の使い分け
論文への記載テンプレート（Methods & Results）
まとめ

はじめに

医療論文を読んでいると、このような解析結果をよく目にしませんか？

群A vs 群B
群A vs 群C
群B vs 群C
それぞれで p < 0.05 だったので、すべてに有意差あり！

「 p 値が0.05を切っているなら、何回比較しても問題ないのでは？」と思ってしまいがちですが、ここに多重比較（multiple testing）の落とし穴があります。

実は、検定を繰り返せば繰り返すほど、私たちは**「統計学的な嘘」**をついてしまうリスクが高まっていくのです。

多重比較とは何か？

一言でいうと、多重比較の問題とは**「比較を何回も行うことで、本当は差がないのに『差がある』と判定してしまうこと」**です。

ポイントは、データに本当の差がなくても、比較回数が増えるだけで「偶然の当たり」が出やすくなるという点にあります。

有意水準5%の本当の意味

統計検定でよく使われる「有意水準 5%」とは、裏を返せばこういう意味です。

「本当は差がない場合でも、20回に1回は“差がある”と誤判定してしまう」

ここで重要なのは、この5%という確率は**「1回の検定」に対するリスク**だということです。1回なら5%で済みますが、これを何度も繰り返すとどうなるでしょうか？

t検定を繰り返すと何が起こるのか？

比較回数が増えるにつれて、偽陽性（本当は差がないのに有意と判定されること）が少なくとも1回は起きてしまう確率がどのように変化するか、以下のデータを見てみましょう。

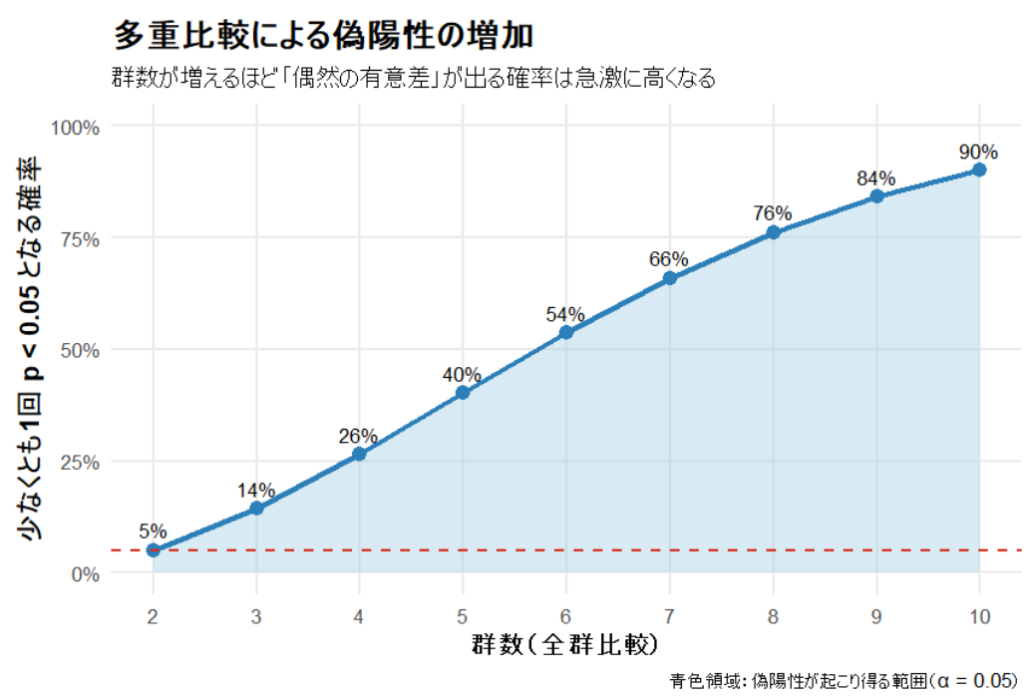
【図1：多重比較による偽陽性の増加】

図の見どころ

横軸： 群数（全群比較を行う場合）
縦軸： 少なくとも1回 p < 0.05 となる確率

グラフを見ると、比較が増えるにつれて偽陽性率は急激に上昇しているのがわかります。

2群（比較1回）： 偽陽性率は 5%。これは設定通りです。
3群（全比較）： 確率は 14% まで上がります。
5群（全比較）： なんと 40%。
10群（全比較）： 実に 90%！

つまり、10個のグループを総当たりで比較すれば、たとえ薬に全く効果がなくても、**ほぼ確実に「どこかに有意差が出てしまう」**のです。

特に医療分野では、この「偶然の差」を治療効果だと誤解してしまうと、効果のない治療を患者さんに推奨してしまうリスクにつながります。これが**多重比較による偽陽性（false positive）**の恐ろしさです。

このような比較群が多いときの偽陽性を予防するために、多重比較法と呼ばれる手法があります。

「多重比較問題」と「多重比較法」を区別しよう

ここで用語を整理しておきましょう。

多重比較問題： 比較が増えることで偽陽性が増えてしまう**「現象・リスク」**
多重比較法（事後比較法）： それを防ぐための**「対策・計算テクニック」**

つまり、多重比較法（Bonferroni法やTukey法など）は、結果を厳しくするために使うのではありません。**「偶然の当たりを、実力だと勘違いしないため」**に使うのです。

「ANOVAをやっていれば安心」ではない

「最初に分散分析（ANOVA）で全体を検定しているから、その後の比較は自由だ」と思われがちですが、これは半分正解で、半分誤りです。

ANOVAが答えてくれるのは、**「どこかの群に差があるか？」**という大まかな問いだけです。

その後に、「具体的にAとBに差があるか？」と個別比較を行う段階（事後検定）では、やはり多重比較の問題が再燃します。そのため、事後検定専用の手法が必要になるのです。

ノンパラメトリック検定でも必要？

「うちはノンパラ（Kruskal-Wallis検定など）だから大丈夫」という声をたまに聞きますが、結論から言うと、必要です。

分布の形に関わらず、「何度もクジを引けば当たりが出る」という確率は変わりません。事後比較を行う限り、多重比較の補正は必須の手順です。

代表的な多重比較法（事後検定）の使い分け

「結局、どの方法を使えばいいの？」と迷ったときは、**「何を、何と比較したいのか」と「データの性質（分散）」**で選びます。

初めて多重比較に触れる方が迷ったら以下の表を参考にしてください。

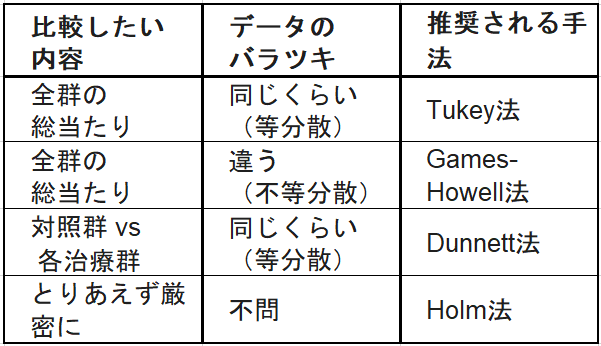
ここから先は各多重比較法について個別に紹介していきます。

1. Bonferroni（ボンフェローニ）法

「最もシンプルで厳格な門番」

どんな方法か？：有意水準（0.05）を比較回数で割るだけの非常にシンプルな方法です。
前提条件：特になし（どんな検定の組み合わせにも使えます）。
長所：計算が簡単で、どんな場面でも使える「汎用性」が魅力。
短所：比較回数が増えると判定が厳しくなりすぎる（保守的すぎる）ため、本当は差があるのに「有意差なし」と判定されやすい。

2. Holm（ホルム）法

「ボンフェローニの進化系」

どんな方法か？：ボンフェローニ法を少し賢くした方法です。p値が小さい順に並べ、段階的に有意水準を変えて判定します。
前提条件：特になし。
長所：ボンフェローニ法よりも**「有意差が出やすい（検出力が高い）」**。現在はボンフェローニの上位互換として推奨されることが多いです。
短所：手計算だと少し面倒（統計ソフトを使えば一瞬です）。

3. Tukey（テューキー / Tukey–Kramer）法

「全群比較の王道」

どんな方法か？：3群以上のグループ間で、**すべての組み合わせ（総当たり）**を比較したいときに使います。
前提条件：各群の分散が等しい（等分散性）こと。
長所：全組み合わせを比較する際、ボンフェローニ法よりも正確で有意差を検出しやすい。
短所：群ごとのバラツキ（分散）が大きく違う場合には使えません。

※TukeyのHSD（Honestly Significant Difference）法というものもあります。
これは「各群のサンプルサイズ（人数）がすべて同じ」であることを前提として作られた手法です。最近の統計ソフトであれば、サンプルサイズによって自動的にTukeyのHSD法と Tukey–Kramer法を切り替えてくれるようです。

4. Dunnett（ダネット）法

「対照群（コントロール）との比較に特化」

どんな方法か？：特定の「対照群（コントロール）」と、他の「治療群A、B、C…」をそれぞれ比較する方法です（例：プラセボ vs 新薬低用量、新薬中用量、新薬高用量）。
前提条件：各群の分散が等しいこと。
長所：総当たり（Tukey）をしない分、対照群との比較において高い検出力を持ちます。
短所：治療群同士（A vs Bなど）の比較はできません。

5. Scheffé（シェッフェ）法

「どんな比較も許す慎重派」

どんな方法か？：2群間の比較だけでなく、「A群 vs (B群+C群の平均)」といった複雑な比較（対比）も可能です。
前提条件：各群の分散が等しいこと。
長所：あらゆる組み合わせを試しても偽陽性を抑えられる。
短所：全手法の中で最も判定が厳しい。単純な2群間比較のために使うと、有意差はほとんど出ません。

6. Games–Howell（ゲームズ・ハウエル）法

「バラツキが違ってもOKな実力派」

どんな方法か？：Tukey法の弱点を克服した方法です。
前提条件：等分散でなくても（群ごとのバラツキが違っても）OK。
長所：医療データに多い「群によって人数が違う」「バラツキがバラバラ」という状況でも安心して使えます。
短所：サンプルサイズ（n数）が極端に少ないと不安定になることがあります。

論文への記載テンプレート（Methods & Results）

多重比較を行った際、論文の本文や図表にどのように記載すればよいか、具体的なテンプレートを用意しました。

1. 統計解析（Methods）の記載例

解析手法を説明するセクションでは、**「どの検定の後に」「どの多重比較法を使ったか」**を明記します。

【日本語での記載例】

3群以上の比較には一元配置分散分析（one-way ANOVA）を行い、事後検定として**[手法名：Tukey法など]**を用いて群間比較を行った。有意水準は両側5%未満とした。

【英語での記載例】

Statistical significance was determined using one-way ANOVA, followed by [手法名：Tukey’s, Dunnett’s, etc.] post hoc test for multiple comparisons. A p-value < 0.05 was considered statistically significant.