はじめに
今回は、無料の統計ソフト「JASP」を使って探索的因子分析をたった40秒で実行します。
さらに仮定のチェック+因子負荷量+パス図の出力まで一気に行う方法を紹介します!
統計ソフトを使って分析をする、というとなんだか難しそうですよね?
たしかに難しいソフトもありますが、最近の統計ソフトは使いやすくなっています。
JASPは操作がシンプルなので、統計が初めての方でもすぐに使えます。
なお、「JASPってなに?」と思った方は、こちらの記事でJASPの紹介をしています。
まずは、この動画(40秒)をご覧ください。
最初に、全体の流れをつかむため、こちらの動画をご覧ください。
このように40秒で、探索的因子分析の実施からパス図作成までできました。
探索的因子分析(Exploratory Factor Analysis:EFA)とは
探索的因子分析とは、
複数の質問項目の背後にある共通の構造(因子)を、データから探索的に見つけ出す統計手法です。
心理学・教育学・看護学などの分野では、質問紙データを扱うことが多く、
卒業論文や修士論文でも非常によく使われています。
例えば次のような質問があるとします。
- 人前で話すと緊張する
- 緊張すると心拍が速くなる
- 些細なことで不安になる
- 心配事が頭から離れない
これらは一見別々の質問ですが、
背後には「不安」「緊張」といった**共通の心理特性(潜在変数)**が存在している可能性があります。
探索的因子分析は、
このような「目に見えない共通因子」をデータから推定するための方法です。
「探索的」という言葉の意味
探索的因子分析では、次の点を事前に仮定しません。
- 因子はいくつあるのか
- どの質問項目がどの因子に属するのか
つまり、
「このデータには、どんな因子構造が潜んでいるのだろう?」
という問いに対して、
**データ主導で構造を探る(探索する)**のが探索的因子分析です。
これに対し、
因子数や構造をあらかじめ仮定して検証する方法は
**確認的因子分析(CFA)**と呼ばれます。
探索的因子分析と主成分分析の違いは?
探索的因子分析(EFA)と主成分分析(PCA)は、次の点で「そっくり」に見えます。
- 多数の変数を 少数の次元(因子・成分)にまとめる
- 相関行列(または共分散行列)を使う
- 固有値・スクリープロットが出てくる
- 因子負荷量/主成分負荷量という「寄与の強さ」を見る
- 回転(PCAでも数学的には可能)という概念がある
なので
👉 JASPの画面や結果表だけ見ると「ほぼ同じ分析」に見える
これは本当に自然な混乱です。
では何が違うのでしょうか?
探索的因子分析では、**想定されるモデルの中に「独自因子」**が含まれています。
イメージ的には以下のようなものです。
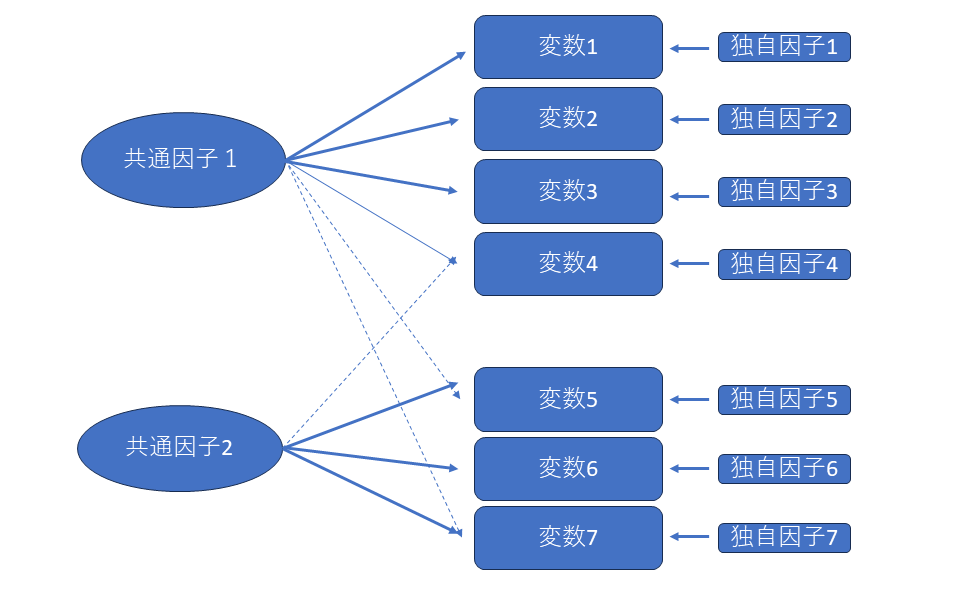
各観測変数は、
- 複数の変数に共通する 共通因子 と
- その変数特有の 独自因子(誤差・固有要因) から成り立つ
という考え方を取ります。
つまり因子分析では、
共通の背景因子が存在し、その結果として複数の変数が観測されている
という因果的なモデルを暗に想定しています。
一方、主成分分析のモデルイメージは以下のようなものです。
主成分分析では独自因子や誤差項を明示的に分離するモデルは採用しません
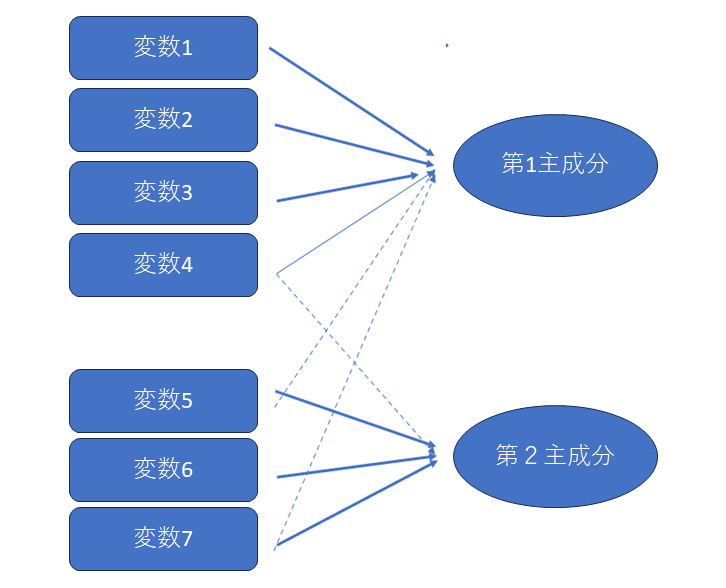
主成分分析では各変数が持つ情報(分散)をできるだけ すべて主成分に盛り込む ように数学的に再配分する、という立場を取ります。
そのため主成分分析は、
「誤差を分離する」というよりも 「情報を失わずに要約する」
ことに主眼が置かれています。
この モデルの考え方の違い を理解しておくと、
- なぜ因子分析では平行分析(FAベース)を使うのか
- なぜ PCA と同じ感覚で因子数を決めてはいけないのか
といった点が、より納得しやすくなります。
JASPで探索的因子分析を実行する流れ
ここから先は以下の流れで、JASPの実際の操作手順を紹介します。
- データの準備・読み込み
- 探索的因子分析の実行
- 因子負荷量やパス図などの出力設定
- 外部出力
以下、設定項目ごとにおすすめの考え方を解説します。
今回使用するデータ
探索的因子分析を始める前に、まずはデータをJASPに読み込む必要があります。QOL評価を想定したサンプルデータを使います。
データは以下のようなものです。JASPはcsvファイル・Excelファイル(.xls .xlsx)に対応しています。
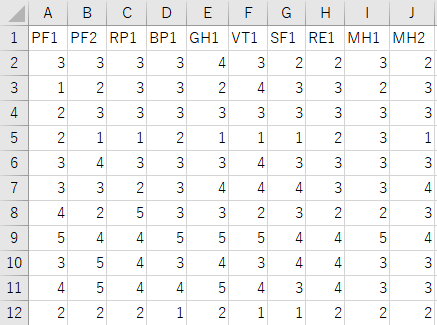
行ごとに症例ごとのデータが横並びに記載されています。各列の先頭には列名が入力されています。分析に使用する列は後から指定できるため、ID列などが残っていても構いません。
PF(身体機能)
RP(役割・身体)
BP(痛み)
GH(全体的健康感)
VT(活力)
SF(社会生活)
RE(役割・精神)
MH(心の健康)
これらは医療の現場でよく用いられる評価指標です。
なお、データの準備段階で一つ注意点があります。日本語の列名や特殊文字は文字化け・エラーの原因になることがあります。半角英数で列名を記載するようにしましょう。
※今回使用するデータは統計ソフトで機械的に生成されたものです。実際の臨床象を反映したものではありません。ご注意ください。
JASPでのデータ読み込み手順
- JASPを起動し、左上の File メニューから開く→コンピュータ→参照を選びます。

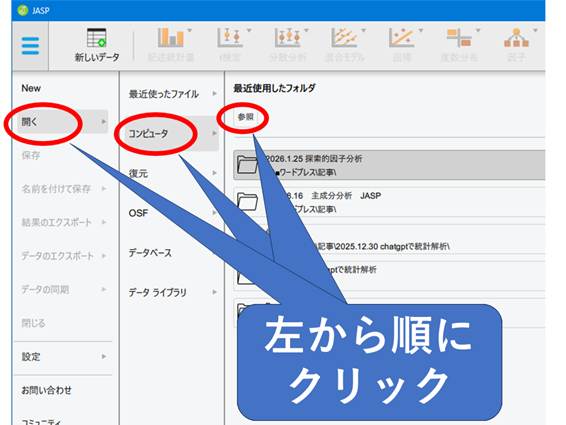
- 保存してあるCSVファイル(Excelファイル)を指定すると、JASPのデータビュー画面に表形式でデータが読み込まれます。
- データ確認のポイント
読み込んだ直後には、次の点を簡単に確認しておきましょう。
- 変数名 が正しく表示されているか
- 欠損値(空欄)がないか
- すべての解析対象変数が数値データになっているか
とくに探索的因子分析は数値データを前提とした手法なので、文字列データ(例:男/女、あり/なしなど)が混ざっていないか注意が必要です。このようなデータは(男性/女性→1/0)のようなダミーデータに置き換える必要があります。
探索的因子分析の実行(JASPでの手順)
データが問題なく読み込めたら、いよいよ探索的因子分析を実行します。JASPではマウス操作だけで設定できるため、プログラミングの知識は不要です。画面上部のメニューから因子→探索的因子分析とクリックしてください。
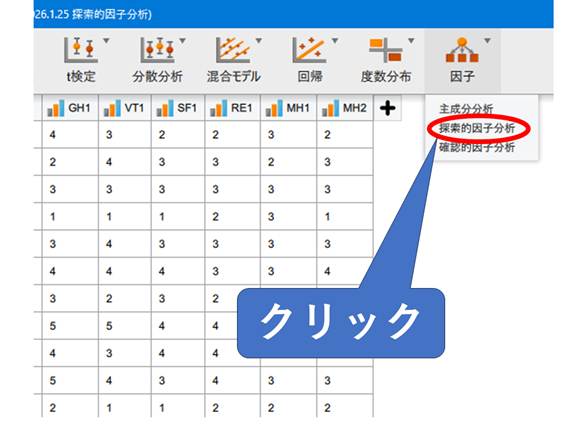
因子分析のメニューを選ぶと以下のような画面になります。
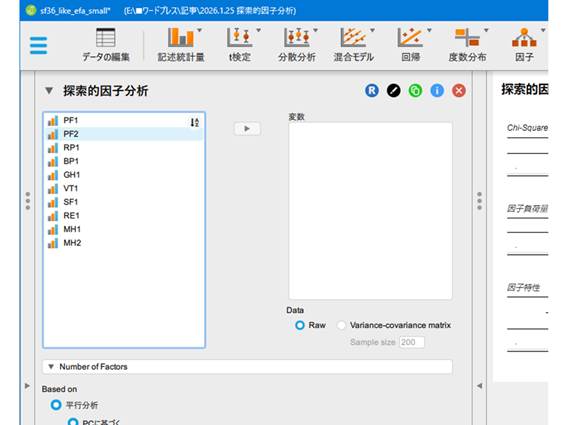
変数の選択
解析に使う変数を指定します。左の枠にある変数群から使用するものを選択し、右側の変数欄にドラッグ&ドロップで移動します。
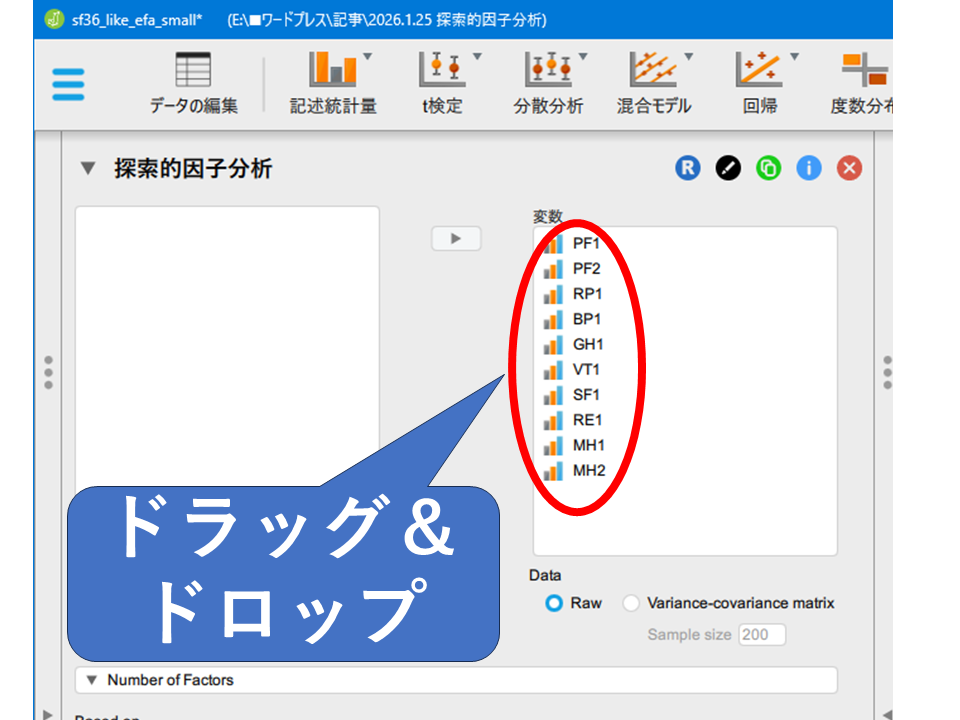
変数枠へ項目を移動するとすぐに解析結果が右の出力ウィンドウに出てきます。
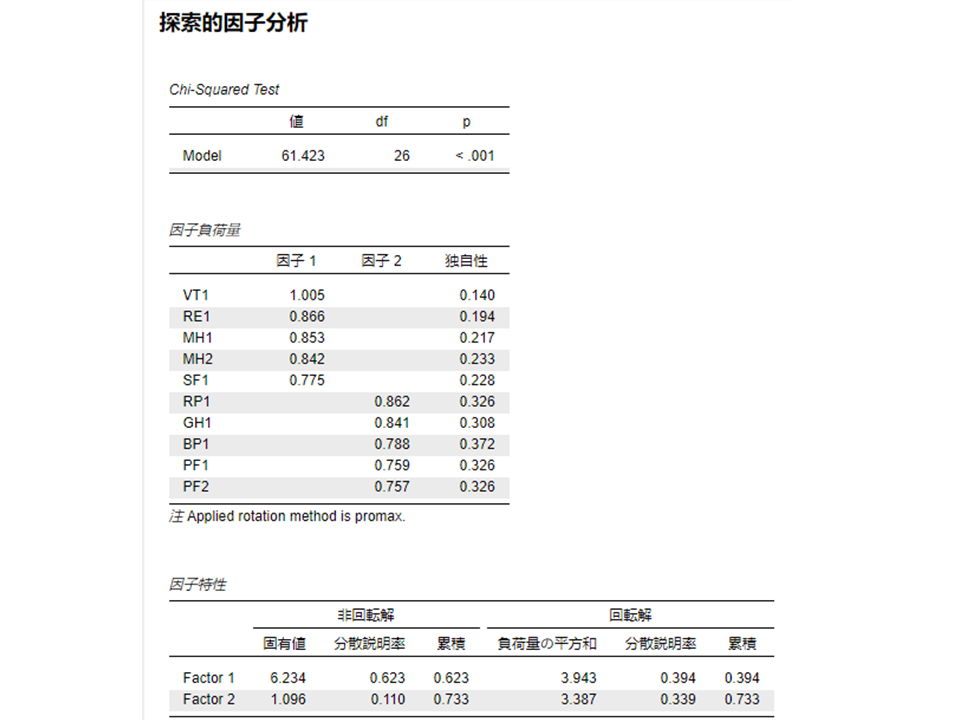
分析設定のポイント
今回の分析では以下のオプションを指定しています。
- 次に基づく成分数→平行分析
- KMO検定
- Bartlettの検定
- 平行分析(平行分析の結果を見る場合にチェックします)
- パス図
- スクリープロット
因子数の決定に関する項目は「Number of Factors」タブで行います。
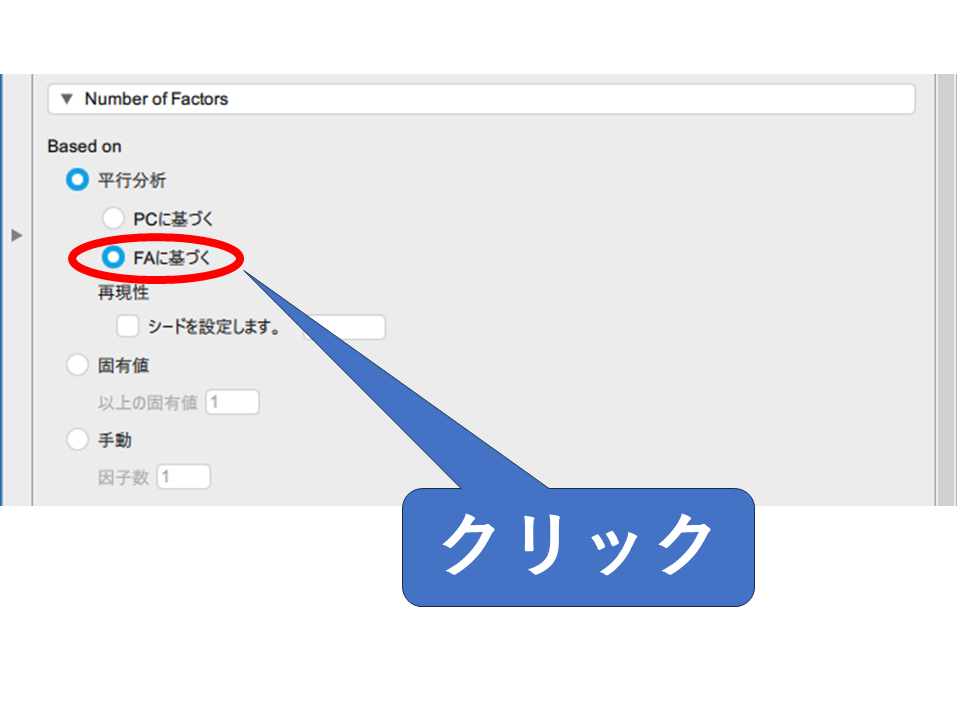
因子数の選択方法は、平行分析・固有値・手動の中から選択できます。
今回は信頼性が高いとされる、平行分析を選択します。この時「FAに基づく」をチェックしましょう。「PCに基づく」をチェックすると、主成分分析をベースにした解析が実行されてしまいます。
また、平行分析ではランダム生成したデータをもとに結果が出力されるため、実行ごとに結果が変わります。出力を固定したい場合は、「シードを設定します。」にチェックを入れて、特定の数値を右枠に入力しましょう。数値が同じであれば、同じ出力がされます。
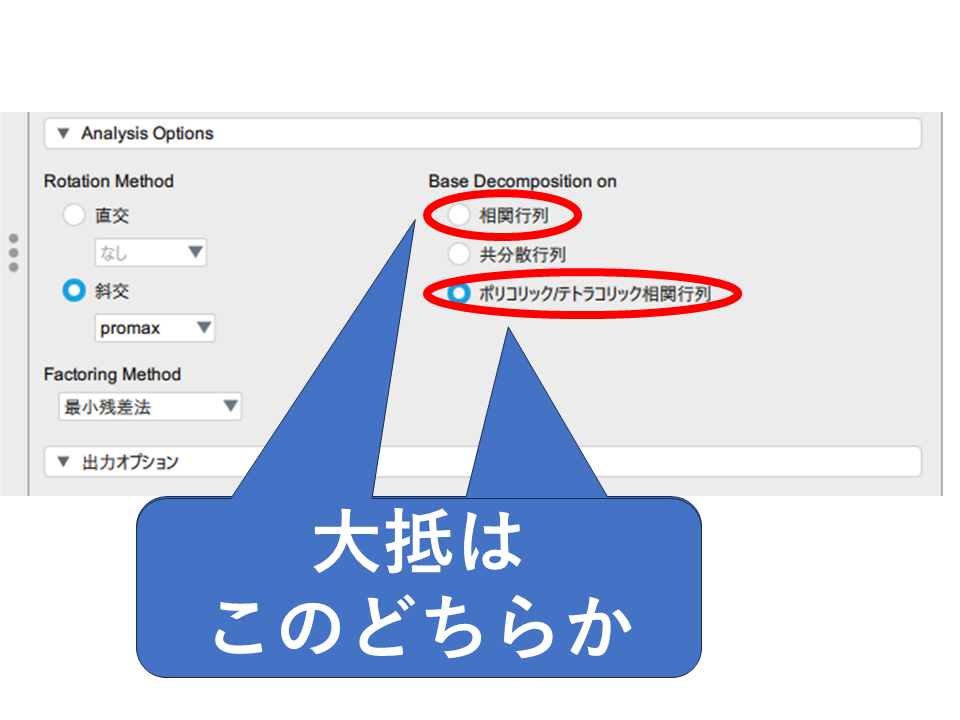
「分析に用いる行列の項目」ですが、ざっくりとした選択基準は以下のようになります。
- 相関行列:データの単位による数値の大きさを無視して公平に扱いたい時(身長、体重、筋力で解析など)
- 共分散行列:家計における項目ごとの金額のように、項目間の数値の大小の影響を残したい時(食費、交際費、通信費など)
- ポリコリック/テトラコリック相関行列:順序尺度の解析の時
回転について
主成分分析では、回帰分析の下処理として実施することもあり、主成分同士の相関が出ないようにする事(直交回転を使用)が多いかもしれません。
一方、探索的因子分析では、因子間の相関が全くないということは稀であり、斜交回転が選択されることが多いと思います。
JASPの初期設定では、プロマックス回転が選択されています。プロマックス回転は計算が早いものの、理論通りの解が出ないこともあるようです。気になる場合はoblimin回転など、ほかの手法を検討してもいいかもしれません。
※参考:清水 優菜 研究に役立つ JASPによる多変量解析 – 因子分析から構造方程式モデリングまで 2021
解析はこれで完了です。
右の出力ウィンドウに順次結果が出力されているはずです。
結果の解釈
JASPで探索的因子分析を実行すると、因子負荷量、残差、パス図などの結果が表示されます。ここでは、仮定の庭の確認法と因子数の決め方について説明します。
探索的因子分析の仮定の確認(KMO・Bartlett検定)
JASPではKMO・bartlett検定のオプションが用意されています。探索的因子分析は変数間の相関を仮定としており、相関がほとんどない場合は意味のある共通因子を抽出できません。その確認に使えるのが、 Kaiser-Meyer-Olkin(KMO)検定 と Bartlettの球面性検定 です。
KMO検定とは
KMO検定は、各変数が他の変数とどれだけ相関しているかを評価する指標です。値の目安は次の通りです。
- 0.8以上:非常に適している
- 0.7前後:適している
- 0.6未満:探索的因子分析には不十分
KMOの値が高いほど、探索的因子分析による次元縮約が有効であると判断できます。
Bartlettの球面性検定とは
Bartlettの検定は、変数間の相関がほとんどない(=単位行列である)という帰無仮説を検証します。
- p < 0.05 であれば、変数間に十分な相関があると判断でき、探索的因子分析を適用可能です。
出力結果の例
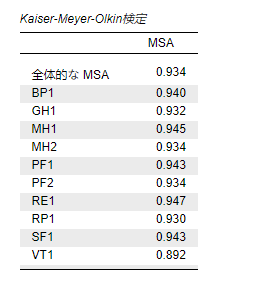
今回の例では、すべての変数で0.8を上回っているため、KMO検定から主成分分析に適したデータであることが分かります。
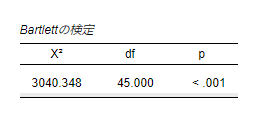
Bartlettの検定でもp<0.05であり、変数間の相関が無いことが否定されるため、主成分分析に適したデータであることが示されています。
必要な場合は、こういった検定を使用して、データが探索的因子分析に適しているか判断しましょう。
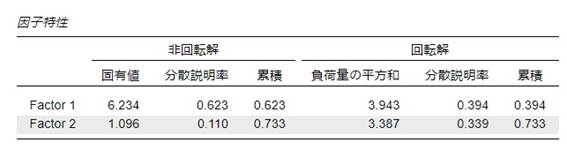
固有値と寄与率(分散説明率)
固有値は主成分がどれだけの情報(分散)を説明しているかを示す指標で、寄与率(分散説明率)はそれを割合で示したものです。例えば今回のサンプルでは以下の通りです。
因子数の決め方
共通因子としていくつの因子を抽出するかは、解析者が分析の用途や結果を考慮して決めます。目的に応じて複数の決め方があり、以下のような方法と特徴があります。
累積寄与率
- 判断方法:累積寄与率が 50~60%以上を目安に、データの特徴を主成分として十分抽出できていると判断する。
- 最近はあまりいい方法とはされていない。
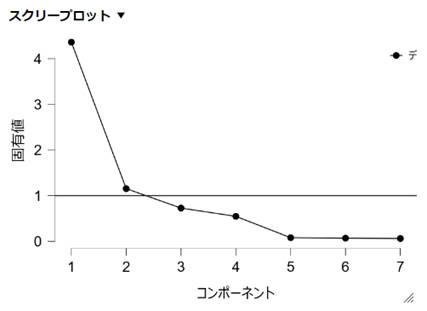
スクリープロット
- 判断方法:固有値を大きい順に並べてグラフ化し、折れ曲がり(エルボー)の位置で打ち切る。グラフがなだらかになるひとつ前までの共通因子を残すことが多いようです。このグラフでは、コンポーネント2あたりからなだらかになっている為、その前の共通因子1(コンポーネント1)のみを残すという判断になります。
- 適した用途:探索的な分析に適する。心理学・社会学などで、データの背後にある因子数を直感的に把握したいとき。
固有値1以上の基準(カイザー基準)
- 判断方法:標準化データの場合、固有値が1以上の主成分を残す。
- 適した用途:心理測定・教育測定などの古典的な研究で補助的に利用。近年は残しすぎる傾向があるため、他の基準と併用されることが多い。
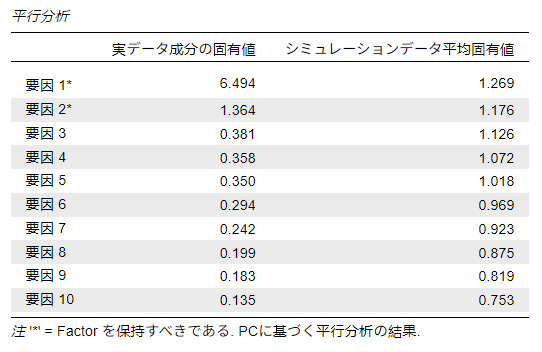
例えば、今回のデータを見てみると、シミュレーションデータよりも固有値が高いのは要因1の6.494のみです。要因2の固有値は1.364でシミュレーションデータの1.176よりも低い値となっています。この場合は、シミュレーションデータよりも高い固有値である、要因1のみを共通因子として採用することになります。
平行分析
- 判断方法:ランダムデータから得られた固有値と比較し、実データの固有値が大きい因子だけを残す。
- 適した用途:心理学・社会科学などで因子数を決める標準的な方法。信頼性が高く、探索的因子分析でもよく用いられる。
手動で指定
- 判断方法:分析目的に応じて主成分数をあらかじめ決める。
- 理論的に因子数が決まっている場合や、先行研究によりすでに因子数がわかっている場合は手動で指定することも可能。
結果の外部出力
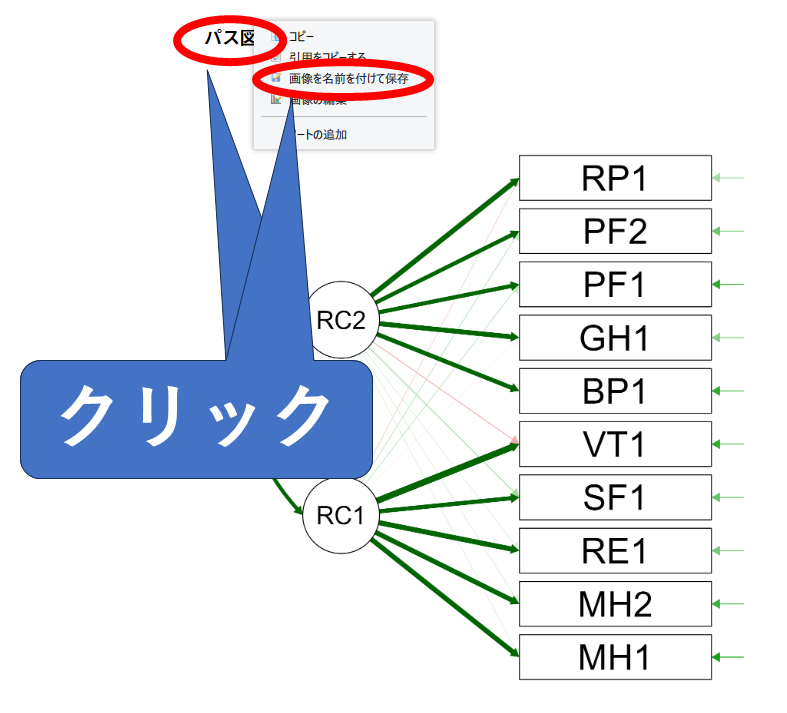
グラフを保存する場合:
表やグラフを保存することもできます。
グラフの場合は、グラフタイトルをクリックしてメニューを出します。そこから「コピー」をクリックしてWordやPowerPointなどのソフトに貼り付けるか、「画像を名前を付けて保存」をクリックして好きなフォルダに保存しましょう。
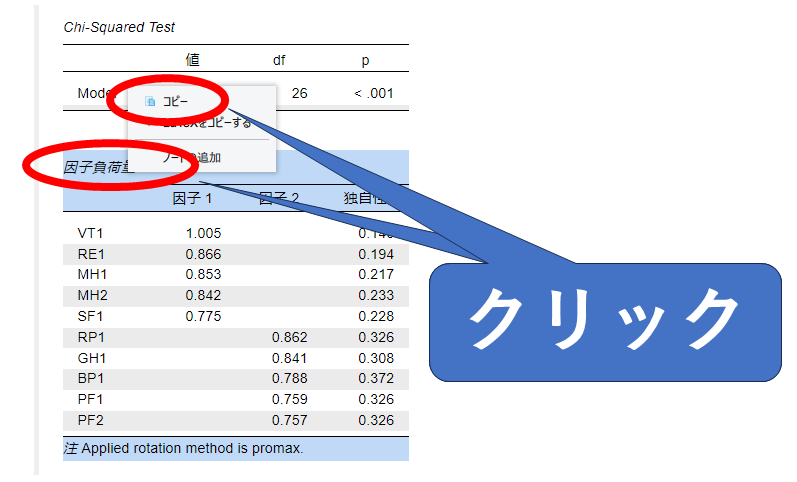
表を保存する場合:
こちらもグラフと同様です。表のタイトルをクリックするとメニューが表示されます。「コピー」を選んで、WordやPowerPointなどのソフトに貼り付けてください。貼り付けた後は編集することもできます。
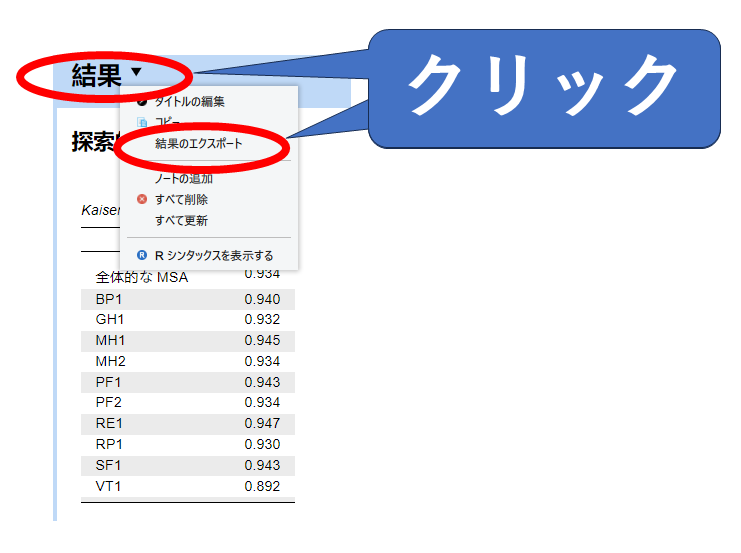
結果全体を出力する場合:
結果全体を出力する場合は「結果」をクリックするとメニューが表示されます。そこから結果のエクスポートを選択します。出力形式はHTMLかPDFが選べます。
まとめ
本記事では、無料の統計ソフト JASP を用いて、探索的因子分析(EFA)を実行する方法を解説しました。
探索的因子分析は、複数の質問項目の背後にある 共通の構造(潜在因子) をデータから推定するための手法で、心理学・教育学・医療分野の質問紙データ解析で広く用いられています。
JASPを使えば、
- KMO検定・Bartlett検定による前提条件の確認
- 平行分析による因子数の決定
- 因子負荷量・スクリープロット・パス図の出力
といった一連の流れを、プログラミング不要で直感的に実行できます。
特に 「FAに基づく平行分析」 を選択することで、因子分析の考え方に沿った因子数決定が可能になります。
探索的因子分析では、結果を機械的に読むのではなく、
因子構造や因子の意味が理論・先行研究と整合しているかを考えることが重要です。



コメント