統計やデータサイエンスにおける回帰分析で、避けて通れない問題の一つが「多重共線性」です。なんとなくは理解していても、実務でどの程度気にすべきか迷うことはありませんか？
今回は、意図的に相関のあるデータを生成し、多重共線性が予測モデルの性能や係数の安定性にどのような影響を与えるかを実験的に検証しました。
基礎知識の復習
多重共線性とは？
多重共線性（Multicollinearity）とは、回帰分析において複数の説明変数（独立変数）の間に強い相関関係がある状態を指します。回帰分析は変数間に相関がないことを前提としているため、この前提が崩れると精度や解釈に悪影響を及ぼします。
具体例として、床面積・部屋数・築年数から住宅価格を予測するモデルを考えてみましょう。この場合、「延床面積」と「部屋数」には強い正の相関があると考えられます。面積が広ければ部屋数も多くなる傾向があるためです。
このように変数間に強い相関があるときに、多重共線性がある、と言います。多重共線性があると、以下のようなデメリットが生じます。
- 回帰係数の不安定性：わずかなデータの変化で係数が大きく変動する
- 係数の解釈が困難：各変数の真の効果を正しく把握しにくくなる
- 統計的有意性の低下：本来有意であるべき変数が有意でなくなる
- 予測精度の低下：新しいデータへの汎化性能が落ちる可能性がある
VIF（分散拡大係数）とは？
VIF（Variance Inflation Factor）は、多重共線性の程度を定量的に評価する指標です。各説明変数を他の変数で回帰し、その決定係数（R²）から以下の式で求められます。
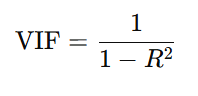
VIFによる多重共線性の判断の目安として、以下のような基準が一般的です。
- VIF = 1：相関なし（理想的）
- VIF ≒ 5：中程度の多重共線性（注意）
- VIF ≒ 10：強い多重共線性（要注意）
- VIF > 10：非常に強い多重共線性（対策必須）
R²・RMSEとは？
- R²（決定係数）：モデルが目的変数の分散をどれだけ説明できているかを示す指標。1に近いほど良好。
- RMSE（Root Mean Square Error）：予測値と実測値の誤差の平均的な大きさ。値が小さいほど予測精度が高い。
偏回帰係数とは？
偏回帰係数は、他の説明変数を変化させずに、ある変数が1単位変化したときの目的変数の変化量を表します。多重共線性が強いと、この係数の推定が不安定になり、解釈の信頼性が低下します。
検証の手順
相関のあるデータの生成
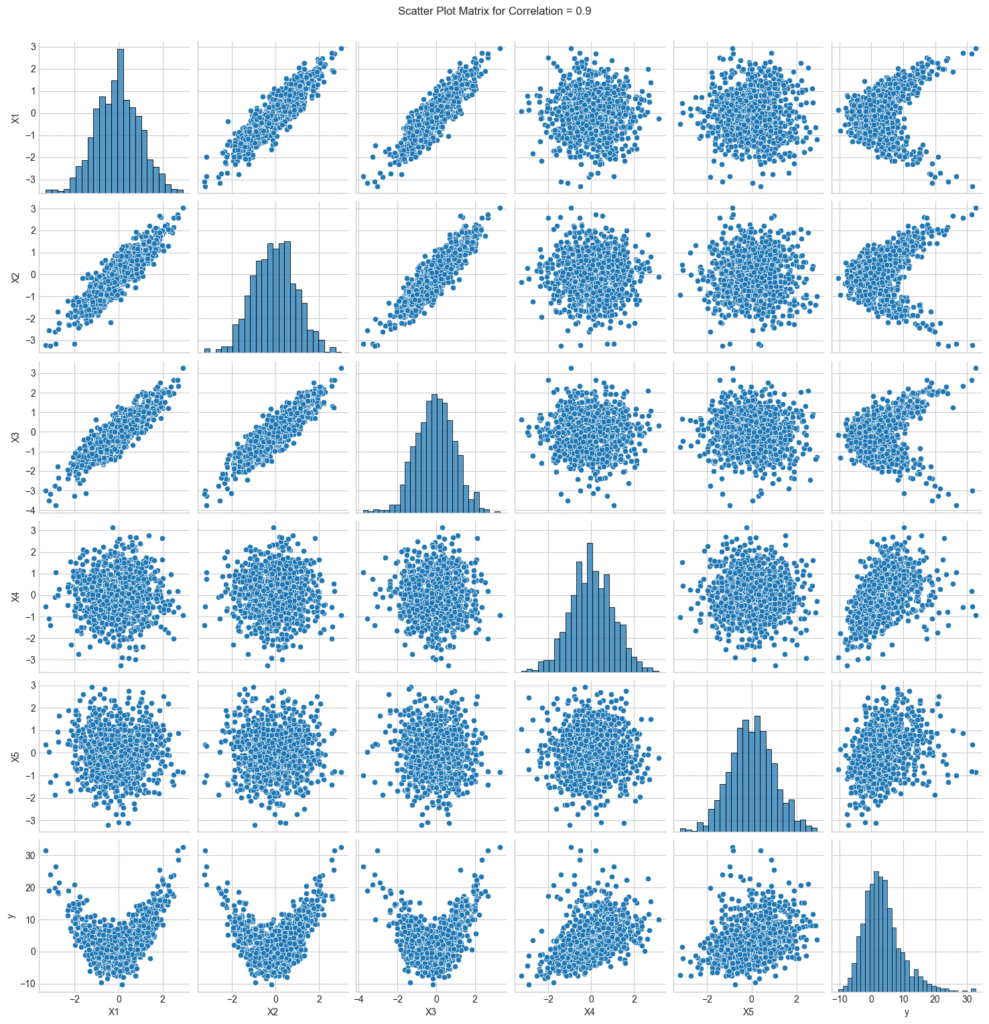
5つの独立変数（X1〜X5）と1つの従属変数（y）からなるデータセットを生成しました。X1〜X3 の間に意図的な相関を設定し、その強さをパラメータで制御できるようにしています。相関がないデータでは、X1とX2に曲線的な関係をもたせています。相関が0.9のときの散布図では、変数間の強い相関が明瞭に確認できます。
こちらは相関係数0の状態。
こちらは変数X1～3までに相関係数0.9の相関を持たせた状態。散布図行列の左上に強い相関がある様子が確認できます。
多重共線性の影響の検証
相関係数を段階的に変化させながら、各パターンについて複数回の試行を行いました。
各試行では、まずデータをサンプリングし、それを用いて重回帰モデルを学習させたうえで、その性能をR2とRMSEで評価しました。さらに、モデルの係数がどの程度安定して推定されているかを確認するために、偏回帰係数の標準偏差を算出しました。
多重共線性の程度を数値的に把握するために、各説明変数についてVIF（分散拡大係数）も併せて算出しています。
最後に、記録された結果をまとめて、3つのグラフで可視化し、相関度合いの変化が各指標に与える影響を確認しました。
検証してみて分かったこと
① 推定精度はやはり下がる
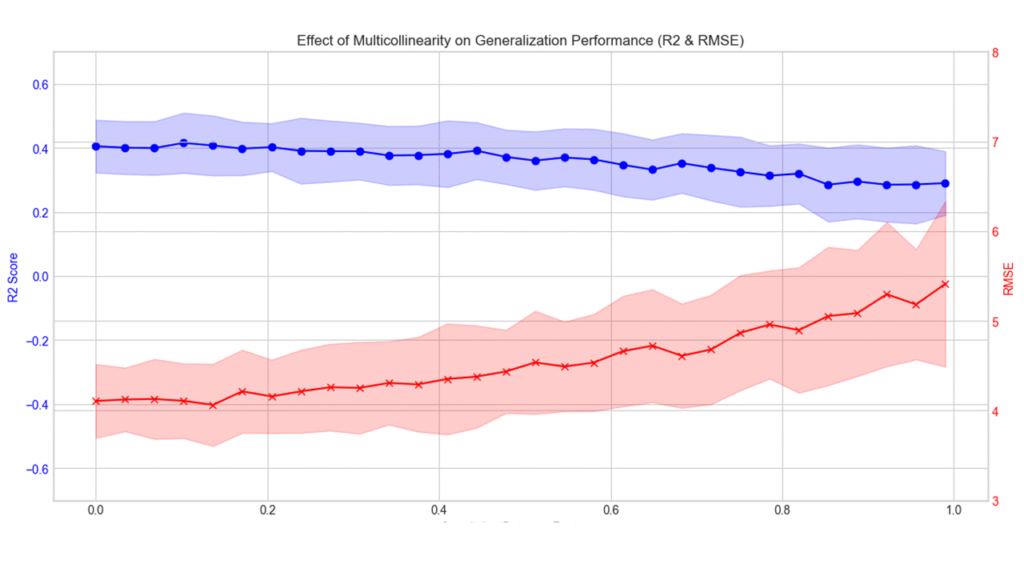
以下の2つのグラフは、それぞれ400件と50件のサンプルで回帰分析を行った場合のR²（青）とRMSE（赤）です。
サンプル数400で回帰分析
サンプル数100で回帰分析
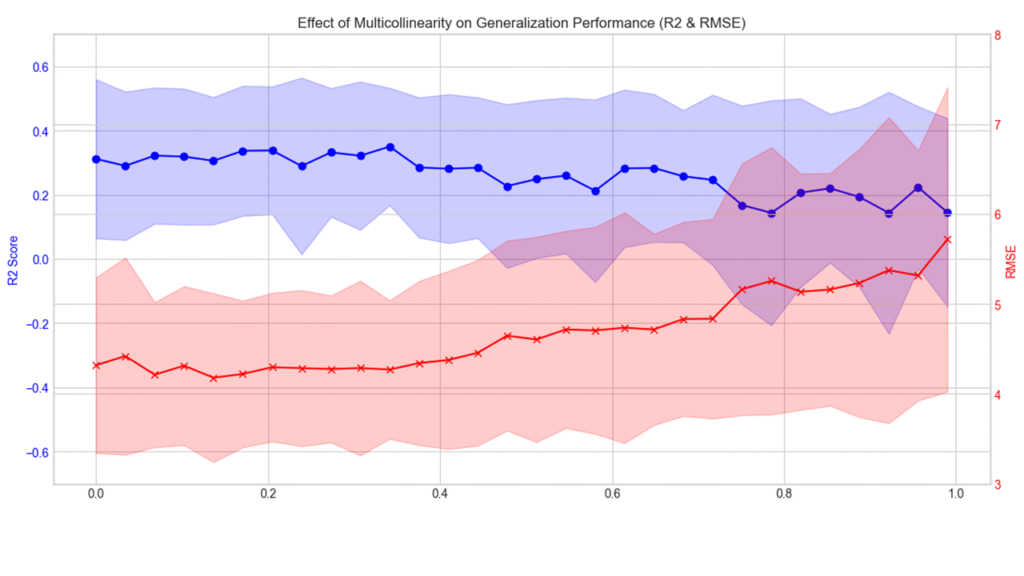
相関係数が高くなるにつれ、精度の平均が悪化しています。また、相関係数が高くなるにつれR²・RMSEの試行ごとのばらつきが広がり、標準偏差も大きくなっています。これは推定結果の不安定性が顕著化することを示しています。
特にサンプル数が少ない場合もとの推定精度が低いため、多重共線性による精度の低下が致命的になり易いようです。
② 偏回帰係数のばらつきの変化
以下のグラフはX1～5の説明変数の偏回帰係数の推定値の不安定性を記録したものです。
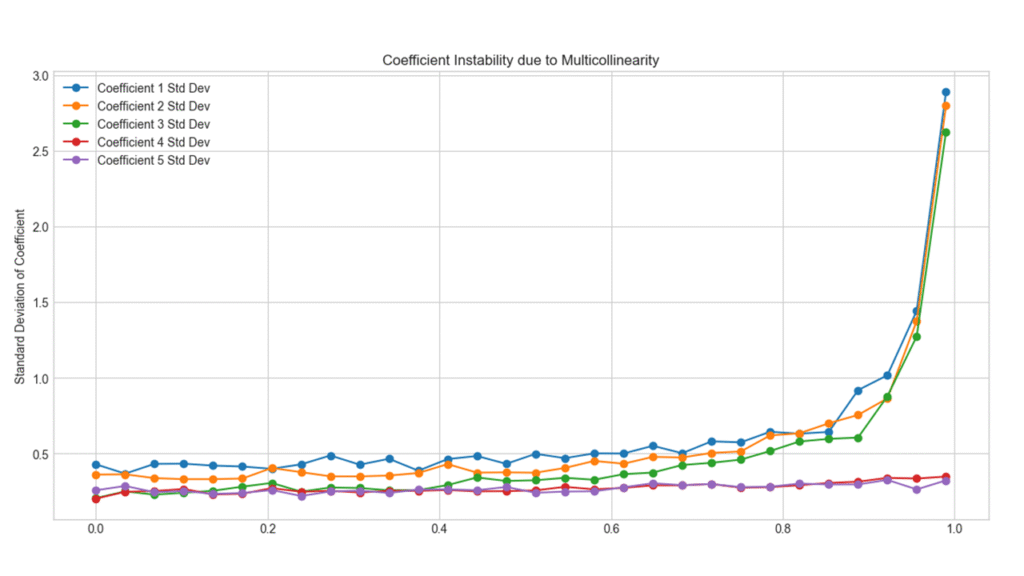
相関係数0.5を超えるあたりから、偏回帰係数の標準偏差が顕著に増加しています。特に相関係数が0.8を超えたあたりから、推定精度が急激に低下するようです。これは回帰分析に使用するサンプル数を変更しても同様の傾向でした。
相関が高くなるほど非線形に影響が大きくなるようです。相関をもたないX4, X5では、当然ですが一貫して安定した推定結果が得られました。
なお、青と黄色のラインは非線形データ、緑のラインは線形データを示しています。最終的な精度の低下量はあまり変わりません。しかし線形データの方が元の精度が良い分だけ、倍率で見れば精度の悪化が大きくなります。
③ VIFと係数ばらつきの関係
以下のグラフは相関係数ごとの偏回帰係数のばらつきとVIFの値のグラフを並べて表示したものです。縦のラインが分かりやすいように縦線を追加しています。
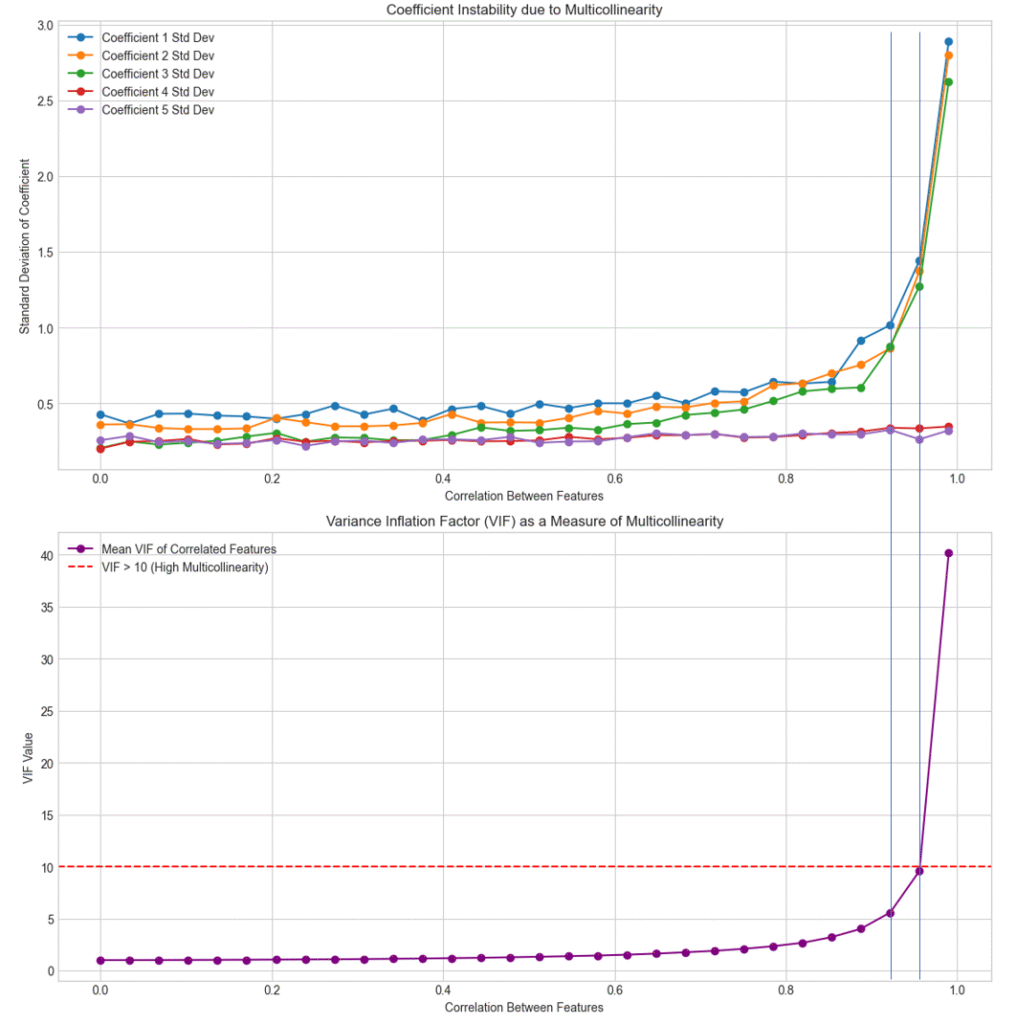
偏回帰係数のばらつきが数倍に膨らんでも、VIFはまだ5程度のようです。一般に「VIF＞5なら注意が必要」と言われます。このレベルでもすでに推定精度には悪影響が出ており、精度は変数間の相関がない場合の数分の一になっている可能性があるようです。
VIFが10を超えると、偏回帰係数のばらつきは3〜6倍程度にまで拡大しています。一般的な「VIF ＞ 10なら多重共線性はかなり強い」という基準は間違いではないです。このレベルまで行くと推定精度は相当下がっていると考えていいでしょう。
まとめ
影響の強さは条件次第
相関係数が0.5程度であれば、モデルの実用価値が大きく損なわれるほどの影響は観察されませんでした。変数間の独立性が高く変数間に複雑な相関関係が無い場合であれば、それほど過敏にならなくても良いかも知れません。
なお、今回は説明変数5つ中、相関があるのは3つという設定でした。実際に分析行う実世界のデータと比べると、非常に単純なデータと言えます。変数の数や相関構造によっては、影響がより深刻になるケースもあり得ます。たとえば2変数間の個別の相関が0.5程度でもVIFは高くなる、という場合があるため油断は禁物です。
実践的な対応指針
- 多重共線性は主に「係数の不安定性」として問題になる
- VIFでの判断はやっぱり妥当。VIFが5を超えたらモデルの精度は数分の1になっており、VIFが10を超えたら精度は1/5程度以下になっている可能性がある。
- サンプル数が多ければ影響を抑えられるが、変数調整の方が現実的
- 特に解釈重視の業務（医療・金融・政策など）では注意が必要
多重共線性は確かに回帰分析において重要な問題ですが、その影響は段階的に現れます。実務では、VIFなどの指標を活用して適切にモニタリングしつつ、モデルの目的や要求精度に応じて柔軟に対応することが求められます。
理論と実践のバランスを取りながら、データの特性を理解し、賢くモデリングを進めていきましょう。
コメント