はじめに:リスク比とオッズ比、どちらも「比」だけど実は違う
臨床研究や論文を読んでいると、「オッズ比(Odds Ratio:OR)」や「リスク比(Risk Ratio:RR)」という言葉をよく見かけます。
どちらも「ある要因が病気やイベントの発生にどのくらい関係しているか」を示す“比”ですが、実は定義も意味も異なります。
特に、オッズ比は直感的に理解しにくいため、「リスク比と同じようなもの」と誤解されることも少なくありません。
この記事では、リスク比とオッズ比の違い、使い分けの理由、そして発症率によって両者の値がどのように変化するのかを、図とともにわかりやすく解説します。
また、「発症率が低ければオッズ比はリスク比に近似する」と言われますが、
では実際にどれくらい低ければ“近似”するのか?
その疑問を確かめるために、具体的なグラフを作って検証してみました。
リスク比とは?:危険度の直感的な比較
リスク比(Risk Ratio, RR) は、2つの集団での発症率(リスク)を比較する指標です。
たとえば、
- 喫煙群の肺がん発症率:10%
- 非喫煙群の肺がん発症率:2%
であれば、
RR = 10%/2% = 5
つまり、「喫煙者は非喫煙者に比べて5倍肺がんになりやすい」と解釈できます。
直感的に理解しやすく、「危険度の倍率」を表すのがリスク比です。
オッズ比とは?:確率をオッズに変換した比
一方の オッズ比(Odds Ratio, OR) は、「発症する確率」と「発症しない確率」の比であるオッズを使います。
オッズ = 発症する確率/発症しない確率
上の例にあてはめると、
- 喫煙群のオッズ:0.10 / 0.90 = 0.111
- 非喫煙群のオッズ:0.02 / 0.98 = 0.020
OR = 0.111/0.02 = 5.55
このように、リスク比よりやや大きな値になります。
この「リスク比より大きく見える」性質が、後ほど紹介する“乖離”の原因になります。
2×2表で見る違い(具体例で理解)
リスク比とオッズ比は、2×2表を使うと整理して考えやすくなります。
| 発症した | 発症しなかった | 合計 | |
| 曝露あり(喫煙群) | a | b | a+b |
| 曝露なし(非喫煙群) | c | d | c+d |
- リスク比: RR = (a / (a+b)) ÷ (c / (c+d))
- オッズ比: OR = (a/b) ÷ (c/d)
リスク比は「発症率の比」、
オッズ比は「発症オッズの比」と覚えると整理しやすいでしょう。
なお、リスク比・オッズ比のもとになる、リスクとオッズはそれぞれ値が取り得る範囲に違いがあります。
リスクは0~1(0~100%)までの範囲に収まります。
一方、オッズは0から大きな値まで広い範囲を取ります。極論すれば100人中99人が発症するのであれば、オッズは99となります。このような点からも、オッズ比はリスク比よりも数値が大きく変化しやすいと言えるでしょう。
なぜオッズ比が使われるのか?:ロジスティック回帰との関係
では、なぜ直感的に理解しやすいリスク比ではなく、やや複雑なオッズ比が論文で多く使われるのでしょうか?
主な理由は次の2つです。
- ケースコントロール研究ではリスクが求められない
発症した群としなかった群を後ろ向きに調べるケースコントロール研究では、母集団全体の発症率(リスク)がわかりません。
そのため、リスク比は計算できず、オッズ比だけが使えるのです。 - ロジスティック回帰分析ではオッズ比が自然に得られる
臨床研究で多用されるロジスティック回帰分析では、モデルの出力が「オッズの対数(log odds)」です。
そのため、解析結果として得られるのはオッズ比であり、統計ソフト(JASP、R、SPSSなど)もオッズ比を標準出力します。
発症率によって変わるRRとORの関係
イベント発生率が低い(たとえば1%未満など)場合、
「発症しない確率」がほぼ1に近くなるため、
オッズ≈リスク
となり、結果的に
OR≈RR
となります。
ちょっと分かりにくいので、先ほどの2×2表を使ってもう一度確認してみましょう。
| 発症した | 発症しなかった | 合計 | |
| 曝露あり(喫煙群) | a | b | a+b |
| 曝露なし(非喫煙群) | c | d | c+d |
リスクとオッズの定義は次のとおりです。
違いがあるのは 赤色の分母の部分 です。
リスク = a / (a+b)
オッズ = a/b
発症率が非常に低いと、a が小さいため b ≈ a+b となります。
その結果、リスクとオッズがほとんど同じ値になり、
リスク比(RR)とオッズ比(OR)も近い値を取ります。
この性質のため、稀な疾患やまれな副作用を対象とする研究では、
オッズ比をそのまま「リスクの倍率」として解釈しても大きな誤差はありません。
しかし、発症率が高くなるとこの近似は崩れます。
たとえば、発症率が30〜50%程度になると、オッズ比はリスク比よりも大きくなり、「リスクが3倍」とは限らない状況が生じます。
つまり、「オッズ比=危険度の倍率」と短絡的に解釈すると、リスクを過大評価するおそれがあるのです。
この点を正しく理解することで、「オッズ比3倍」という表現をより正確に読み解けるようになります。
RRとORの乖離をグラフで視覚的に理解する
以下のようなグラフを描くと、発症率が高くなるほどオッズ比がリスク比よりも大きくなることが一目でわかります。
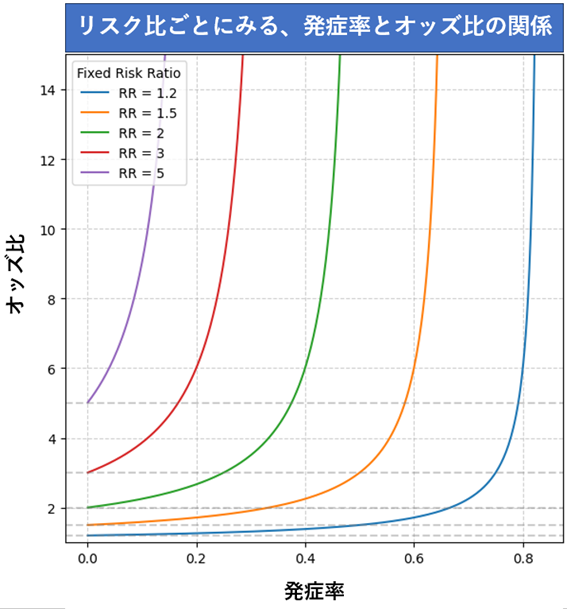
このグラフは、リスク比(RR)ごとに発症率とオッズ比(OR)の関係を示したものです。
低い発症率では、RRとORはほとんど同じ値を取ります。
しかし発症率が10%、30%、50%と高くなるにつれて、オッズ比はリスク比を上回っていきます。
一般に「発症率が低ければオッズ比 ≒ リスク比」と言われますが、そのズレ方はリスク比の大きさによっても変わります。
リスク比が小さい場合は発症率が上がっても差はわずかですが、
リスク比が大きい場合は発症率の上昇に伴って、両者の乖離が急速に広がります。
また、もともとのリスク比が高い場合も、オッズ比との乖離が起きやすいことが分かります。リスク比が1.2や1.5であれば、多少発症率が上がってもオッズ比の変化は緩やかです。
しかし、リスク比が3や5である場合は、少しの発症率の上昇でオッズ比が大きく変化することが分かります。
まとめ:リスク比とオッズ比を正しく理解して論文を読む
- リスク比は「発症率の比」で直感的に理解しやすい
- オッズ比は「発症オッズの比」で、ロジスティック回帰やケースコントロール研究で使われる
- 発症率が低いときはRR ≒ OR
- 発症率が高いときはORがRRよりも大きくなり、リスク比が高いとその傾向が顕著になる。
この違いを理解しておくと、論文の「オッズ比○倍」という表現の意味を正確に捉えられるようになります。




コメント