はじめに
「t検定ってよく聞くけど、種類が多くて混乱する…」
そんな経験はありませんか？
t検定には「対応のあるt検定」「対応のないt検定」「一標本t検定」など、いろいろな呼び名があり、初心者にはわかりづらいのが実情です。この記事では、t検定の種類とそれぞれの使い分け、そして特に混乱しやすい「対応のある」「対応のない」t検定の違いを、直感的にわかりやすく解説します。
なおこの記事では分かりやすさを優先して、厳密さには目をつぶっています。それを踏まえてごらんいただくようお願いいたします。
t検定の種類は3つだけ
t検定には、大きく分けて以下の3つの種類があります。研究では介入前後や介入群・コントロール群で比較する事が多いので、1標本t検定はあまり使われません。この記事では主に下の二つの方法について説明します。
| 検定名 | 目的 | 使う場面の例 |
| 一標本t検定 | 平均値が特定の値と違うか？ | 平均血圧が基準値120より高いか？ |
| 対応のあるt検定 | 同じ対象の前後比較 | ダイエット前後の体重比較 |
| 対応のないt検定 | 別々のグループ比較 | 薬A群と薬B群の効果比較 |
ｔ検定の名前がいっぱいありすぎ
ｔ検定は呼び名が統一されておらず、参考書やサイトによって言い方にばらつきがあります。しかし、実際は同じものを指しています。統計を学び始めた方に混乱を招くため、同じものを下の表にまとめておきます。
| 意味 | よくある表記例 |
| 対応のあるt検定と同じ | 関連2群のt検定 関連のある2標本t検定 関連のあるｔ検定 |
| 対応の無いt検定と同じ | 独立2群のt検定 独立2標本t検定 関連の無いt検定 |
紛らわしいことに上記のような様々な呼び名があります。最近は対応のある・対応のないｔ検定という呼び名が多いようです。この記事でも対応のある・ないという良い方で統一します。
対応のある vs 対応のない t検定：何が違うのか？
対応のないt検定（independent t-test）とは？
別々のグループの平均に差があるかを調べる検定です。
下のようなデータで比較する場合に使用されます。ランダム化比較試験（RCT）もこの検定になります。
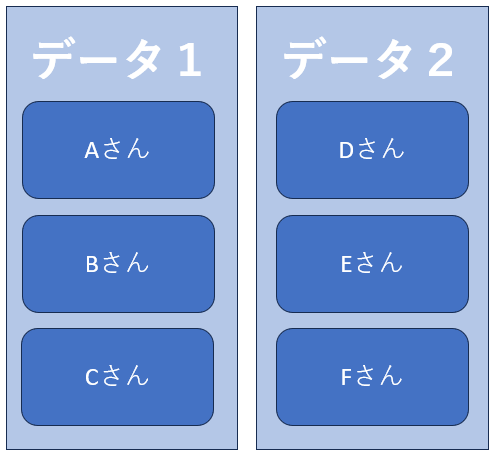
この場合は、単純に平均値の差を見るのではなく、その差がデータのばらつきに比べてどれくらい大きいかを調べます。
ばらつき（分散）の影響を考慮するため、分散が等しいかどうかによって2つのバージョンがあります。
Studentのt検定 vs Welchのt検定
Studentのt検定（等分散を仮定）
両群の分散が等しいという前提（等分散性）をおいた検定です。等分散が成立していれば、こちらの方が検出力が高いとされています。
Welchのt検定（等分散を仮定しない）オススメ
分散が異なっていても使える検定です。等分散性の検定（F検定やLevene検定）を行わずに、Welch検定を使うことが近年では推奨されています。なぜなら、分散が等しいかどうかの検定自体に不確実性があるためです。どちらか迷ったら、等分散性の検定はせずにこちらを使いましょう。
正規性の確認
正規性とはデータの分布が左右対称の山なりになっているかどうか、というものです。いくつかデータの分布のタイプを見てみましょう。正規分布は一番上の山型のデータであり、真ん中や下は正規分布ではない別の分布です。
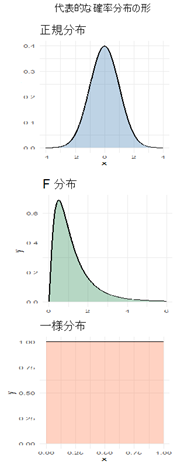
正規性を確認する方法は、大きく2つに分けられます：
– **視覚的手法**：ヒストグラム、Q-Qプロット（実務ではこちらが主流）
– **検定的手法**：Shapiro-Wilk検定（サンプルサイズに敏感なため、補助的に使う）
古典的にはt検定をする前に、データの正規性をShapiro-Wilk検定で確認するというのが習わしでした。
しかし、t検定はもともと非正規性に対して**ある程度頑健**であり、多少分布の偏りがあっても問題にならないことが多いです。
最近では極端な外れ値がない限り、視覚的確認で済ませることも増えています。
なお、この点について興味のある方は「中心極限定理」で調べてみてください。簡単に言えば、サンプルサイズがある程度大きければ、平均値の分布はきれいな形（正規分布）になってくれる、という法則です。以下のサイトが参考になります。
対応のあるt検定（paired t-test）とは？
同じ人や同じ対象において「前」と「後」など、ペアとなる2つの測定値の差をとり、その差がゼロでないかを調べる検定です。
下のようなデータで比較をする場合に使用されます。
このように多くは同一被験者の前後比較などに使用されますが、必ずしも「まったく同じ対象」である必要はありません。生物医学の分野では、以下のように**強く関連するペア**であれば、対応のあるt検定を使うことがあります：
– 異なる環境で育った一卵性双生児の比較
– 同一被験者の右手と左手の測定結果の比較
いずれも「観測単位としての独立性はない」と考えられるため、ペアを前提にしたt検定が使われます。
内部処理としては…
差 = 治療後 − 治療前
上のような計算で求めた「差」の平均値が0かどうかを検定しています。下の画像で言えば対応のあるt検定で分析に使われるのは、介入前・介入後の白い数値ではなく、右側にあるオレンジ色の数値になります。
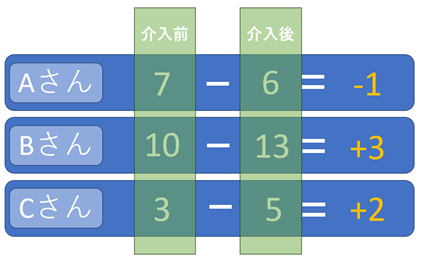
**対応のあるt検定は「差をとって、それを1標本t検定にかけている」**とも言えます。実質的には1標本t検定です。
正規性の確認：どこを確認すべきか？
対応のあるt検定でも、**正規性（データが正規分布に従うこと）**が前提になります。
ここで注意が必要なのは、正規性を確認する対象です。
- 対応のないt検定では、それぞれの群（例：A群・B群）の分布を個別に確認します。
- 一方で、対応のあるt検定では「前」と「後」の差分を計算し、その差の分布が正規であるかを確認します。
つまり、**確認すべきなのは「差を取ったあとのデータ」**です。
この点は混乱しやすいため、意識しておきましょう。
まとめ
- t検定は、「対応のある」「対応のない」「一標本」の3種類
- 「対応のある」t検定は1人ごとの差を使い、「1標本t検定」と同じ考え方で検定する
- 「対応のない」t検定は、2つの独立した群の平均の差を見る
- Welchのt検定は「等分散を仮定しない」ため、現代の実務ではより推奨される
おわりに
統計は「前提条件」や「正しい検定法の選択」がとても大切です。
t検定は身近で便利な手法ですが、どの種類を選ぶかによって、結果の解釈も変わってきます。
「検定の目的」「データの性質」「仮定の成り立ち」を意識しながら、適切なt検定を選びましょう。
実際のt検定のやり方が気になる方へ
最後までお読みいただきありがとうございました本ブログではJASPというソフトを使用した統計解析のやり方を、動画を交えて分かりやすく紹介しています。
ｔ検定のやり方は以下の記事で紹介しています。
【たった30秒】初心者でもできる！JASPでｔ検定＋効果量＋95％CI＋グラフ作成！（対応のある2群）
【たった30秒】初心者でもできる！JASPでｔ検定＋効果量＋95％CI＋グラフ作成！（対応のない2群）
なお、t検定以外の統計手法に興味がある方向けに、以下のページにリンクを貼っています。初心者向けに手法別でわかりやすく解説していますので、ぜひこちらもご覧ください。
👉 JASPの統計手法まとめ記事を見る
コメント