「サンプルサイズが小さいと検出力が下がる」
よく聞く話です。
前回の記事ではt検定について調べてみましたが、思った以上にサンプルサイズの影響が大きいことに驚きました。
そこで今回は、「相関係数の検定(ピアソンのr)ではどうなんだろう?」ということで、同じくRを使って簡単なモンテカルロシミュレーションをしてみました。
やったこと
相関のある架空のデータをコンピュータ上で何度もランダムに生成し、
そこから一定数のサンプルを抜き出してピアソンの相関検定を行いました。
これを繰り返すことで、「そのサンプル数でp値が0.05未満になる確率(=検出力)」を調べました。
あわせて、算出された相関係数がどのようにばらつくのかも確認するため、分布をグラフにしてみました。
今回のシミュレーションの条件
- 検定方法:ピアソンの相関係数(両側検定)
- 母相関係数:0.5(中程度の相関)
- 有意水準:0.05
- サンプルサイズ:n = 5〜50(段階的に変化)
- 検定の繰り返し数:5~50の各サンプルサイズあたり1600回
結果(サンプルサイズと検出力・相関係数の分布)

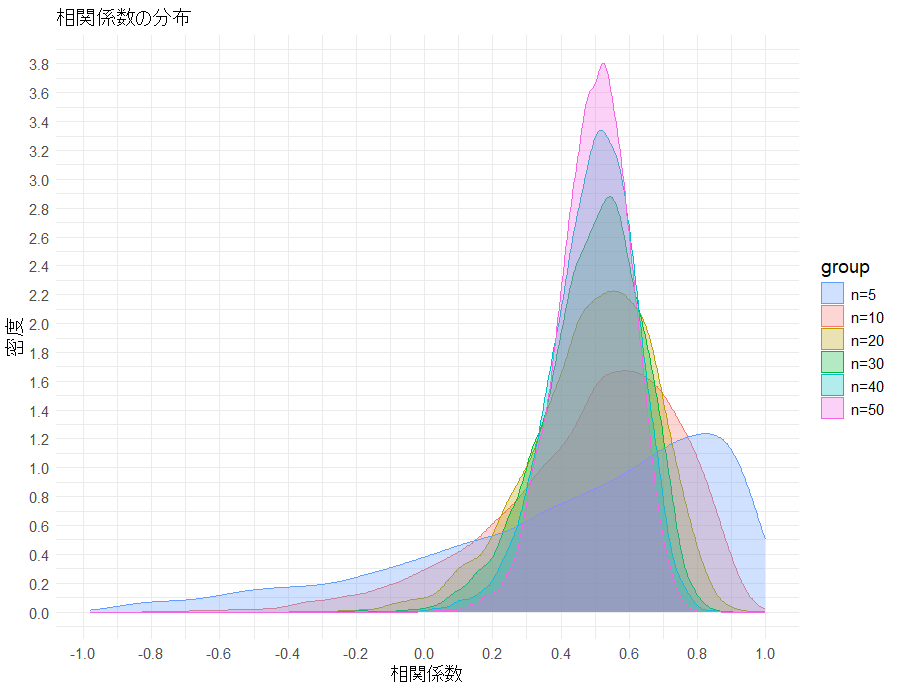
結果から見えてきたこと
結論から言うと、思っていた以上にサンプルサイズが検出力に与える影響は大きかったです。
● 検出力が0.8を超えるのはn = 30前後から
よく「検出力80%以上が望ましい」と言われますが、今回の条件だとサンプル数が30を超えたあたりからようやくそのラインを越える印象でした。
感覚的には、n = 20を超えると「相関ありそう」と言えるようになってきて、n = 30〜40になると「相関係数のアタリがつけられる」といった印象です。
● サンプルが少ないと相関係数の推定が不安定
特にサンプルサイズが10を切るような場合、以下のようなことが見られました:
- 相関係数の推定値が上振れする
- そもそも正負が反転する(本来正の相関なのに負に出る)ことすらある
つまり、小さいサンプルだと「相関があるかどうか」だけでなく、「相関の向きすらブレ得る」状態になります。
リハビリ・医療系の研究ではどう考える?
リハビリや医療領域では、小規模なパイロットスタディも少なくありません。探索的な研究や初期検討としての意義は大きいですが、サンプルサイズが小さいと「たまたま見えた相関」に過剰な意味づけをしてしまうリスクもありそうです。
今回のシミュレーションからも、相関の検定にはある程度のサンプル数が必要であることが改めて実感できました。
結論:相関の検定も、小サンプルはやっぱりキツい
- 検出力0.8を目指すなら、n = 30は欲しい
- n = 20を超えると、相関の存在が少しずつ見えてくる
- n = 10未満は正直あまり信用できない(ブレが大きすぎる)
相関係数の検定においても、t検定と同様、サンプル数の重要性は非常に大きいと感じました。
次に文献を読むときや自分で分析するときに、「その相関、どれくらいのnで言ってるの?」という視点を持ってみると、読み方がちょっと変わるかもしれません。
おまけ:今回使ったRコード
今回のシミュレーションで使用したRコードを載せておきます。
サンプルサイズと検出力・相関係数の推定値の変動を確認する簡単なスクリプトです。
気になる方はぜひ手元で試してみてください。
library(MASS)
library(ggplot2)
# 相関のある2変数のデータを100万行生成
mu <- c(0, 0)
sigma <- matrix(c(1, 0.5, 0.5, 1), nrow = 2)
cor_data <- as.data.frame(mvrnorm(n = 1e6, mu = mu, Sigma = sigma))
# 相関検定を行い、p値を返す関数
cal_cor_p <- function(n){
sampled_rows <- cor_data[sample(1:nrow(cor_data), size = n), ]
test_result <- cor.test(sampled_rows[,1], sampled_rows[,2])
return(test_result$p.value)
}
# サンプルサイズごとに検定を1600回行い、p<0.05の割合を求める
set.seed(123) # 再現性のためにシードを固定
sample_sizes <- 5:50 #調べるサンプルサイズの範囲
trial_num <- 1600 #各サンプルサイズでのp値算出の試行回数
p_less_than_05_ratio <- numeric(length(sample_sizes)) #計算したp値の格納用リスト
for(i in seq_along(sample_sizes)) {
n <- sample_sizes[i]
p_values <- replicate(trial_num, cal_cor_p(n))
p_less_than_05_ratio[i] <- mean(p_values < 0.05)
cat("Sample size:", n, "-> p<0.05:", round(p_less_than_05_ratio[i], 3), "\n")
}
# データフレームに整形
df <- data.frame(
sample_size = sample_sizes,
power = p_less_than_05_ratio
)
# ggplotで折れ線グラフ
ggplot(df, aes(x = sample_size, y = power)) +
geom_line(color = "blue", size = 1) +
geom_point(color = "darkblue", size = 2) +
scale_x_continuous(breaks = seq(5, 50, by = 5)) +
scale_y_continuous(breaks = seq(0, 1, by = 0.1)) +
labs(
title = "サンプルサイズと検出力の関係(ピアソンの相関)",
x = "サンプルサイズ",
y = "検出力(p < 0.05 の割合)"
) +
theme_minimal(base_size = 14) +
theme(panel.grid.major = element_line(color = "grey80"),
panel.grid.minor = element_line(color = "grey90"))




コメント