【初心者向け】線形と非線形の違いをグラフで直感理解

はじめに

統計やデータサイエンスに関する記事を読んでいると、「線形」「非線形」といった言葉をよく目にします。初学者のころ、これらの言葉が何を意味しているのか分かりにくく、戸惑った記憶があります。

先日、ディープラーニングと回帰分析に関する記事を書いた際にも、これらの用語に深くは触れませんでした。しかし、振り返ってみると、「線形」「非線形」の違いは基礎でありながら分かりにくいポイントの一つだと改めて感じました。

そこで今回は、統計や機械学習における「線形」「非線形」という概念について、具体例を交えてわかりやすく解説してみたいと思います。これらの言葉にモヤモヤしていた方の理解の一助となれば幸いです。

注意：この記事では統計・データサイエンス分野での「線形・非線形」について扱います。数学で「線形・非線形」というと加法性・斉次性を満たすもの、となりますがここでは扱いません。

---

線形・非線形とは？

ざっくり言うと、「線形」とは、ある変数が別の変数に対して比例変化する関係を指します。グラフにしたときに直線で表せる関係が「線形関係」です。以下のグラフはすべて線形な関係のデータをグラフにしたものです。

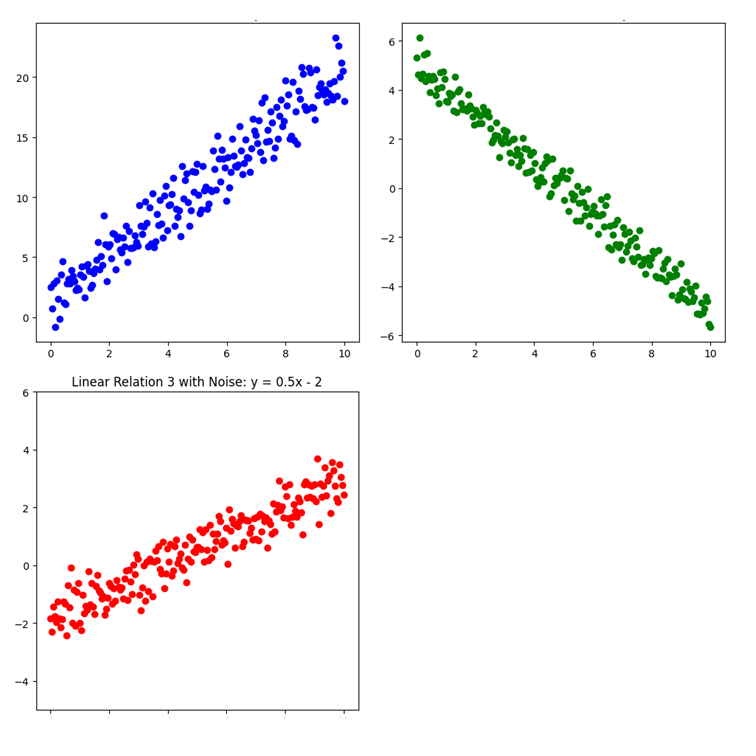
一方で、「非線形」とは、変数同士の関係が直線では表現できない場合を指します。例えば、効果が飽和したり、変化が急激になったりするような関係です。以下のグラフはすべて非線形な関係のデータをグラフにしたものです。

---

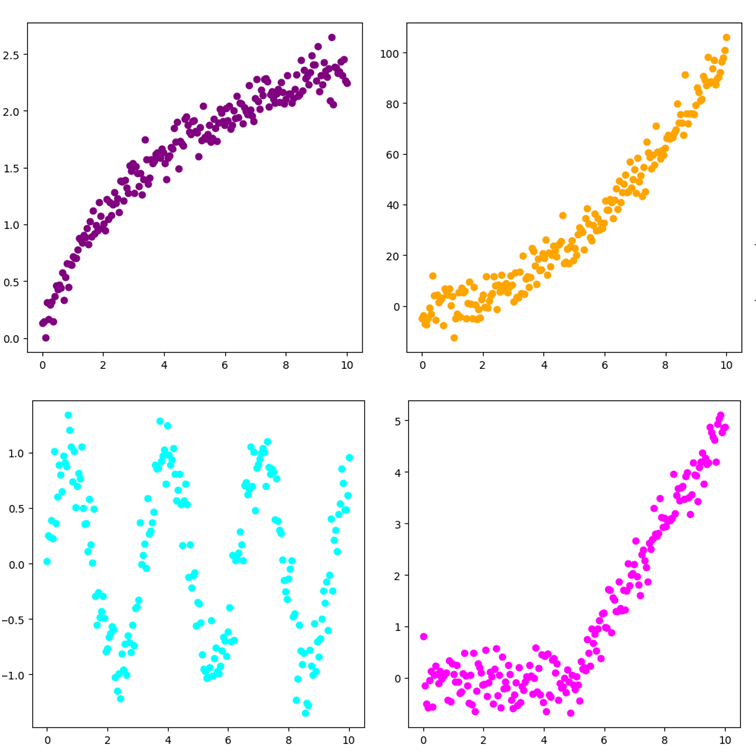
線形・非線形の具体例

線形関係の例

データ例	説明
成人の身長と体重	極端なケースを除けば、一定範囲内で直線的な関係があります。
薬の投与量と血中濃度（初期段階）	投与量に比例して血中濃度が増加する場合、線形とみなせます。
年齢と骨密度（特定年齢層）	50〜70歳など特定の年齢層では、骨密度が年齢とともに直線的に低下する傾向があります。
運動量と消費カロリー	同じペースで運動していれば、2倍運動すると消費カロリーも2倍になります。

非線形関係の例

データ例	説明
薬の投与量と効果	閾値を超えると次第に効果が増すが、一定量を超えると頭打ちになる。
年齢とMMSEスコア（認知機能）	高齢になるにつれて認知機能が急激に低下し、直線では捉えにくい。
リハビリの訓練日数と効果	初期に急激に改善するが、次第に効果が鈍化する（学習曲線）。
心拍数と運動強度	強度が上がると心拍数も上がるが、一定以上には上がらない。
腫瘍サイズと症状	初期段階では無症状だが、閾値を超えると急に症状が出る。
運動負荷量とトレーニング効果	適度な負荷が最も効果的で、負荷が大きすぎても小さすぎても効果が低下する。

医療分野では、

「ある閾値を超えると急に効果が出てくる」

「ある閾値を超えると、徐々に効果が薄れてくる」

といったような非線形関係がよく見られます。

---

文脈による「非線形」の意味の違い

「非線形」という言葉は、使われる文脈によってニュアンスが少し異なります。

• 「非線形なデータ」
  → データの分布やパターンが直線的ではないという見た目・印象に基づく表現。
  例：波のように変動する時系列データなど。
• 「非線形性」
  → より厳密に、変数間の関係の形（モデル構造）を指します。
  例：Xが2倍になるとYが4倍になる → 二次関数的な関係（非線形性）。

この違いを意識すると、論文や解析結果の理解が深まります。

統計学における「線形」とは？

ここまで「線形＝直線的な関係」と説明してきましたが、統計学で「線形」という言葉が使われるときには、少し注意が必要です。

例えば、重回帰分析では、

Y = β₀ + β₁X₁ + β₂X₂ + … + βₚXₚ

のように、説明変数と係数を足し合わせて目的変数を表します。

このようなモデルを「線形モデル」と呼びます。

ここで重要なのは、「線形」というのは、必ずしもデータをグラフにしたときに一本の直線になるという意味ではないということです。

例えば、

Y = β₀ + β₁X + β₂X²

というモデルを考えてみましょう。

X²が入っているため、グラフは曲線になります。しかし、係数 β₀、β₁、β₂に対しては線形なので、統計学では「線形モデル」として扱うことができます。

一方で、

Y = β₀ + β₁e^(β₂X)

のように、未知の係数が指数関数の中に入っているモデルは、「非線形モデル」と呼ばれます。

つまり、統計学では、

「データの関係が直線か曲線か」

と

「モデルが係数に対して線形か非線形か」

は、必ずしも同じ意味ではありません。

ただし、初学者の段階ではまず、

線形モデル：比較的単純な関係を組み合わせて表現するモデル
非線形モデル：より複雑な関係を表現できるモデル

とイメージしておけば十分です。

この違いを意識しておくと、「線形回帰なのに曲線を表現できるのはなぜ？」といった疑問にもつながってきます。

---

線形・非線形データに対応する解析手法

データを調べるときの解析手法も、線形モデル・非線形モデルと言う事があります。線形モデルは変数間の関係を単純化して扱いますが、非線形モデルでは様々な関係性を柔軟に扱うことが出来ます。以下に、それぞれのモデルの特徴と代表的な手法を記載します。

線形な関係を扱うモデルの特徴と手法

• 特徴：
  • 変数間の関係が比較的単純
  • モデルの解釈がしやすい
  • 計算が高速で過学習のリスクが少ない
• 代表的な手法：
  • 線形回帰（Linear Regression）
  • ロジスティック回帰
  • 線形のSVM（サポートベクターマシン）

非線形な関係を扱うモデルの特徴と手法

• 特徴：
  • 複雑な関係性を柔軟に捉えられる
  • 高精度な予測が可能だが、解釈は難しくなりやすい
  • 過学習のリスクがあるため注意が必要
• 代表的な手法：
  • ディープラーニング（ニューラルネットワーク）
  • SVM（非線形カーネルの利用）
  • 決定木・ランダムフォレスト・XGBoostなど

---

線形 vs 非線形が重要な理由

• モデル選択に直結する： 線形関係があるなら単純なモデルで済む
• 前処理・特徴量設計に影響： 非線形性があれば変換（例：対数、2乗）も検討
• 精度と解釈性のバランス： 線形データを想定するモデルは解釈が容易、非線形モデルは高精度だがブラックボックスになりやすい

---

注意点

データが非線形なら必ず非線形関係を想定するモデルを使うべきとは限りません。
たとえば：

• 解釈を重視したい場合は、あえて単純な線形関係を想定するモデルを用いることもあります。
• 線形な関係性のデータに対しても、前処理の違いや臨床でのスクリーニング目的で非線形な関係を想定するモデル（例：決定木）を使うこともあります。

重要なのは、「目的に応じた柔軟な選択」です。

---

まとめ

今回は「線形」と「非線形」の違いについて解説しました。

• 直線で表せる関係は線形データ、それ以外は非線形データ。
• それぞれに対応する解析手法があり、特徴も異なる。
• 解析手法の選択は目的・用途・重視したい点（解釈・予測精度など）に応じて柔軟に考えることが大切。

線形・非線形に関連がある記事

MAE・MSEの使い分け（回帰モデルの評価指標）
Accuracy・Recall・ROC・AUC（分類モデルの評価指標）
ディープラーニングと回帰分析。何が違う？（線形データと非線形データで比較）
LightGBMと回帰分析（サンプル数毎の比較）
ランダムフォレストと回帰分析の比較