はじめに
最近よく耳にするディープラーニング(深層学習)ですが、機械学習の基本的な手法である(重)回帰分析(線形回帰)も、今でも多くの場面で使われています。それぞれの手法は、予測をする時に強力なツールとなりますが、どちらがより適切かはデータの特性によって変わります。
この記事では、ディープラーニングと重回帰分析を使って予測精度を比較し、直線の関係と非直線の関係がどのように結果に影響を与えるかを見ていきます。なお、ディープラーニングの概要について知りたい方はこちらの記事をご覧ください。
※一般にこのような関係を線形・非線形関係と言います。耳慣れない方も多いと思うので、この記事ではそれぞれ直線関係・非直線関係という表現を使います。
予測精度の比較
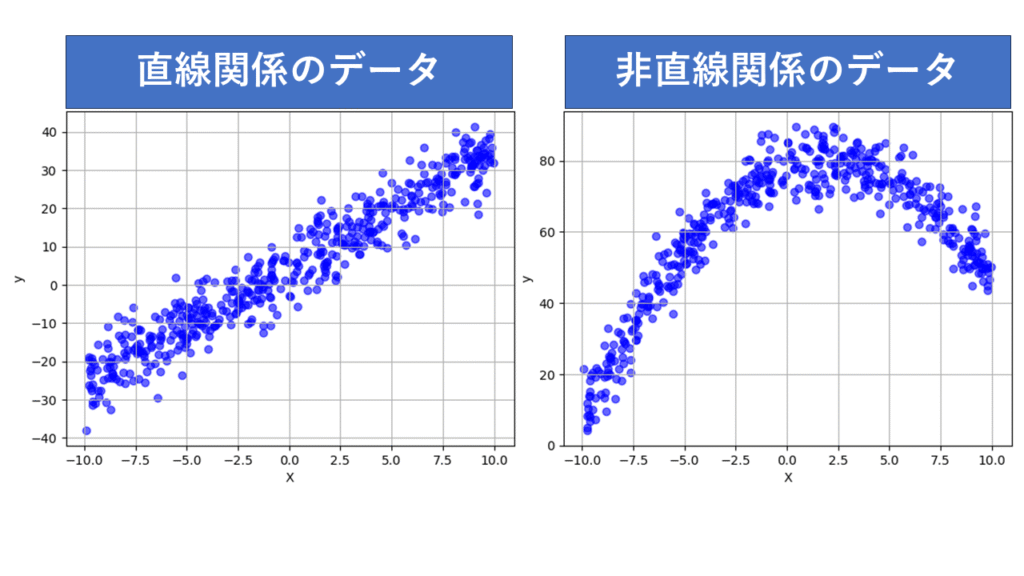
まず、2つの異なるデータセットを用意しました。
・直線関係のデータ:入力変数と予測対象が直線的な関係を持つデータ
・非直線関係のデータ:入力変数と予測対象が曲線的な関係を持つデータ
使用するモデル
予測に使用するモデルは以下の2つです。
- (重)回帰分析
直線関係のデータが得意、直線関係でないデータは苦手。 - ディープラーニングモデル(深層ニューラルネットワーク)
直線関係のデータも、そうでないデータも得意
この二つのモデルを使って、Xからyを予測をしてみようと思います。では、実際にどのモデルがどれくらいの精度を出すのかを見てみましょう。
直線関係のデータの予測精度
まず、直線関係に基づいて生成されたデータを使って、両モデルの予測精度を比べてみました。以下はその結果です。
結果
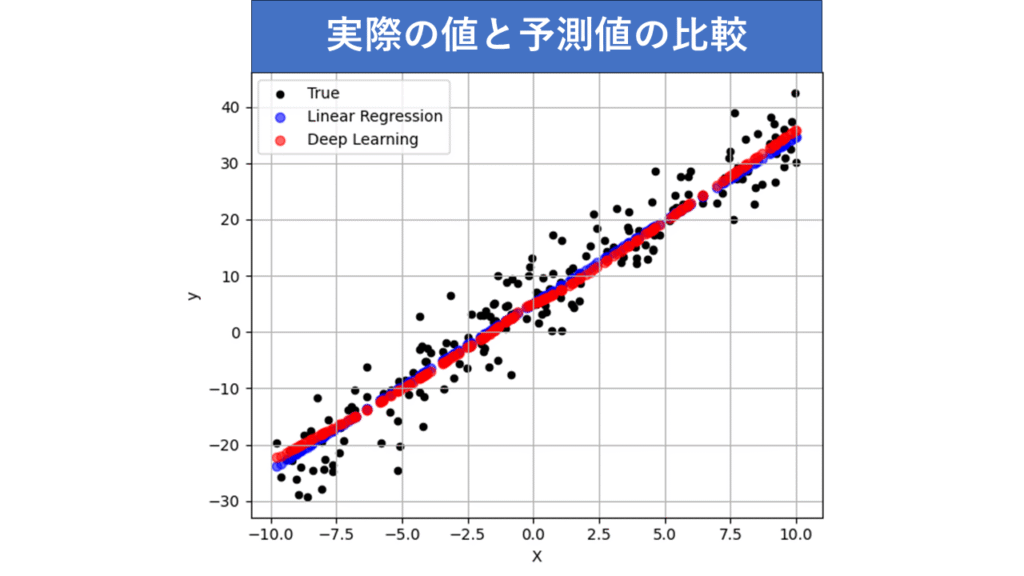
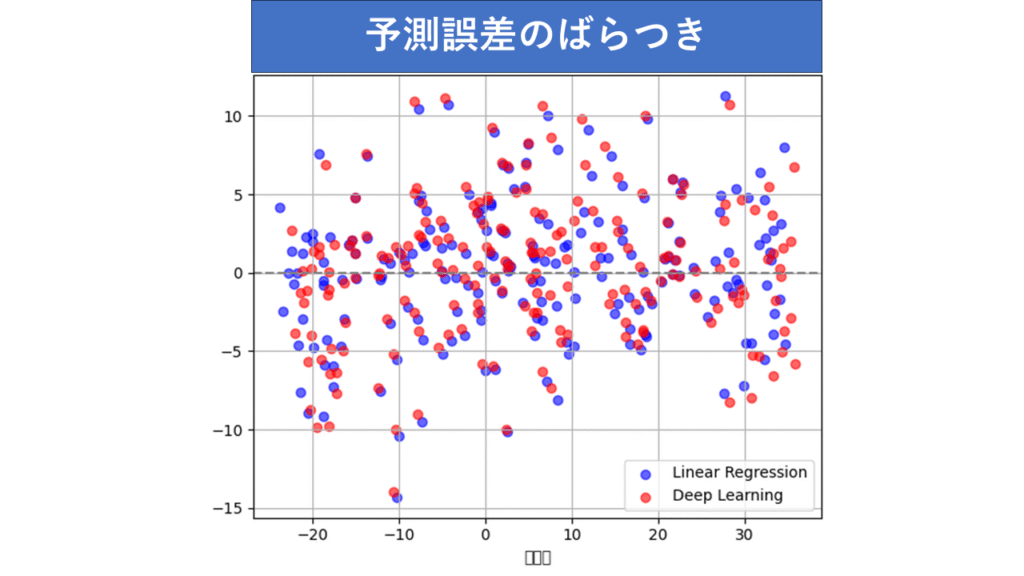
- 回帰分析は、直線関係のデータに対して非常にうまく働きました。予測値はほぼ直線に沿っていて、予測誤差もランダムに分布しています。
- ディープラーニングモデルも高い精度を出しましたが、細かい変動やばらつきをやや敏感に拾い過ぎているようです。
【直線関係のデータにおける予測散布図】
黒:実際のデータ、青:回帰分析の予測値、赤:ディープラーニングの予測値
【直線関係のデータにおける残差プロット】
青:回帰分析の予測値、赤:ディープラーニングの予測値
予測精度の指標の一つである決定係数(R2)も見てみましょう。
1に近いほど高精度に予測が出来ていることになります。予測精度はほとんど同じです。
回帰分析 R² : 0.937
ディープラーニング R²: 0.935
非直線関係のデータの予測精度
次に、非直線関係のデータを使って、両モデルを比較してみました。
結果
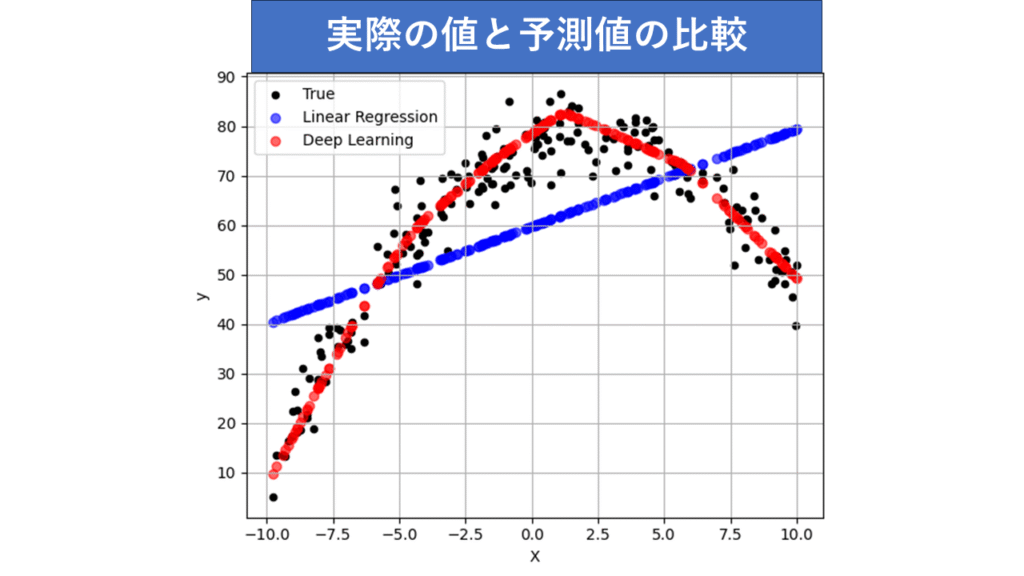
- 回帰分析は、非直線関係のデータに対してはうまく適応できませんでした。実際のデータである黒点が山なりなのに、無理やり直線を当てはめているので仕方ありません。予測誤差のばらつき(グラフ)をみると、半透明の青色表示の予測誤差は山なりのパターンが見られます。これは、直線を想定したモデルが、拾いきれなかったデータの関係性を示しています。
- ディープラーニングモデルは、非直線関係のデータに対して非常に高い予測精度を発揮しました。赤の予測値が、実際の値である黒のデータ群に沿うようになっています。ニューラルネットワークが非直線の関係をしっかり学習した結果です。予測誤差も0を中心に偏りなく散らばっています。
【非直線関係のデータにおける予測散布図】
黒:実際のデータ、青:回帰分析の予測値、赤:ディープラーニングの予測値
【非直線関係のデータにおける残差プロット】
青:回帰分析の予測値、赤:ディープラーニングの予測値
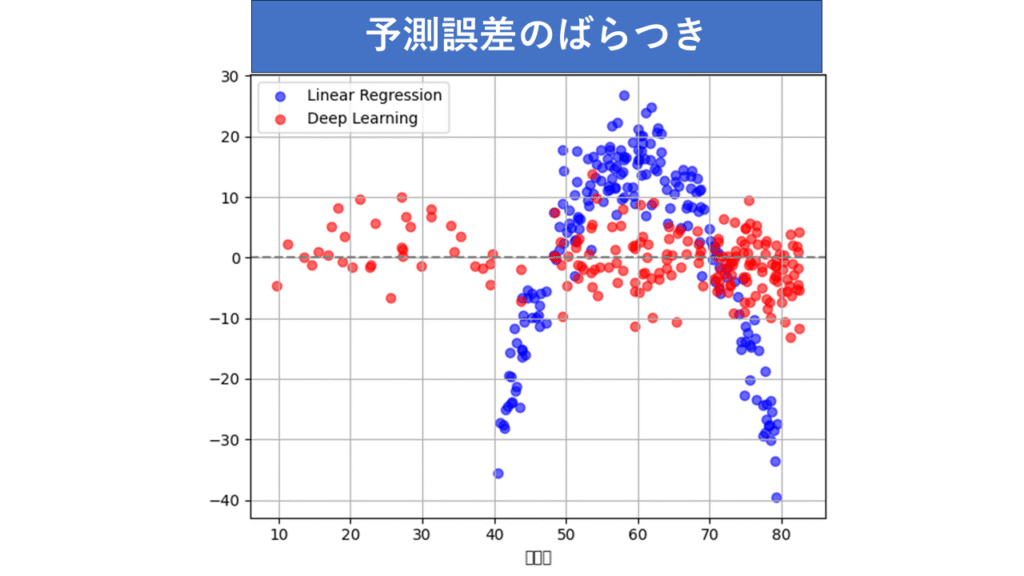
回帰分析のR²はかなり下がってしまいました。回帰分析の予測精度が大きく落ちてしまった結果です。ディープラーニングの方は予測精度を保っています。数字の上でも差があることが分かります。
回帰分析 R² : 0.271
ディープラーニング R²: 0.934
結論
- 直線関係のデータでは、どちらの方法も非常に良い結果を出しました。予測精度は高く、残差も適切に分布しています。一方で、ディープラーニングは少し過剰にフィットしているようでしたが、精度も高いので十分に良い結果が得られます。
- 非直線関係のデータでは、ディープラーニングが非常に優れた結果を出しました。回帰分析は非直線の関係を捉えきれなかったため、予測精度が低くなりました。
この結果から直線の関係があるデータに対しては(重)回帰分析がシンプルで使いやすく、非直線関係を持つデータに対してはディープラーニングが優れた精度を発揮することが分かります。
おわりに
ディープラーニングは複雑な問題に強い一方、データがシンプルな場合にはオーバーフィットしてしまうこともあります。
今回の実験回帰分析の苦手分野だったため、弱さが出ました。しかし、重回帰分析はシンプルで解釈もしやすいため、直線関係のデータにはとても適しています。
データの性質に合わせてどの手法を使うかを判断できると、解析の幅が広がります。興味を持った方はぜひ試してみてください。
参考コード
この記事で使ったコードは以下からご覧いただけます。ぜひ自分で試してみて、どのモデルがどんな結果を出すのかチェックしてみてください!
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# ---------------------------------------------
# データ生成関数(1次 or 2次)
# ---------------------------------------------
def generate_data(func='linear', n_samples=1000, noise_std=5.0):
np.random.seed(0)
X = np.random.uniform(-10, 10, size=(n_samples, 1))
if func == 'linear':
y = 3 * X[:, 0] + 5 + np.random.normal(0, noise_std, n_samples)
elif func == 'quadratic':
y = 0.5 * X[:, 0]**2 - 2 * X[:, 0] + 3 + np.random.normal(0, noise_std, n_samples)
y = -y + 80 # 上に凸で視覚的に分かりやすく
else:
raise ValueError("func must be 'linear' or 'quadratic'")
return X, y
# ---------------------------------------------
# 重回帰モデルで学習
# ---------------------------------------------
def run_linear_regression(X_train, y_train, X_test):
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
return y_pred
# ---------------------------------------------
# ディープラーニングモデルで学習
# ---------------------------------------------
def run_deep_learning(X_train, y_train, X_test):
model = Sequential([
Dense(64, activation='relu', input_shape=(1,)),
Dense(64, activation='relu'),
Dense(1)
])
model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=100, verbose=0)
y_pred = model.predict(X_test).flatten()
return y_pred
# ---------------------------------------------
# 評価とプロット(予測値 + 残差)
# ---------------------------------------------
def evaluate_and_plot(X_test, y_test, y_pred_lr, y_pred_dl, title):
print(f"\n--- {title} ---")
print("Linear Regression R²:", r2_score(y_test, y_pred_lr))
print("Deep Learning R²:", r2_score(y_test, y_pred_dl))
# 1. 予測結果の散布図
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(X_test, y_test, label='True', color='black', s=20)
plt.scatter(X_test, y_pred_lr, label='Linear Regression', color='blue', alpha=0.6)
plt.scatter(X_test, y_pred_dl, label='Deep Learning', color='red', alpha=0.6)
plt.title(f"{title}(予測散布図)")
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(True)
# 2. 残差プロット
residuals_lr = y_test - y_pred_lr
residuals_dl = y_test - y_pred_dl
plt.subplot(1, 2, 2)
plt.scatter(y_pred_lr, residuals_lr, color='blue', alpha=0.6, label='Linear Regression')
plt.scatter(y_pred_dl, residuals_dl, color='red', alpha=0.6, label='Deep Learning')
plt.axhline(0, color='gray', linestyle='--')
plt.title(f"{title}(残差プロット)")
plt.xlabel('予測値')
plt.ylabel('残差(実測値 - 予測値)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
# ---------------------------------------------
# メイン実行部(1次関数 & 2次関数)
# ---------------------------------------------
for func_type in ['linear', 'quadratic']:
X, y = generate_data(func=func_type)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
y_pred_lr = run_linear_regression(X_train, y_train, X_test)
y_pred_dl = run_deep_learning(X_train, y_train, X_test)
evaluate_and_plot(X_test, y_test, y_pred_lr, y_pred_dl, f"関数タイプ: {func_type}")




コメント