前回の記事では、ディープラーニングと重回帰分析の予測精度をサンプル数ごとに比較しました。今回は、ランダムフォレストと回帰分析との比較結果をご紹介します。特に医療データ分析に携わる方々にとって、「どのモデルを選ぶべきか」の参考になれば幸いです。
ランダムフォレストとは?
ランダムフォレストは、複数の決定木(デシジョンツリー)を組み合わせた機械学習モデルです。名前の通り、たくさんの「木」で「森」を作ることで予測精度を高めます。
主な特徴:
- 決定木をベースとしているため、非線形データにも対応できる
- 複数の木の「多数決」で予測するため、単一の決定木より安定した結果が得られる
- SHAP値を用いて各変数の影響度を可視化できるため、ディープラーニングのような完全なブラックボックスではない
医療現場での分析に特に重要な「解釈可能性」という点では、回帰分析ほど単純ではありませんが、ディープラーニングよりは解釈しやすいという中間的な立ち位置にあります。
SHAP値について
SHAP値(SHapley Additive exPlanations)は、モデルの予測結果に対する各変数の貢献度を示す指標です。医療従事者の方にもイメージしやすいよう簡単に説明すると:
- グラフの上に表示される変数ほど、予測への影響が大きい
- 赤い点は、その変数が高い値のとき予測値を上昇させる傾向を示す
- 青い点は、その変数が高い値のとき予測値を下降させる傾向を示す
例えば、「認知機能スコア(MMSE)が高いほど退院時の機能(FIM)が高い」という関係性が赤い点の分布として視覚的に確認できるため、結果の解釈がしやすくなります。
実験の内容
今回の実験では、以下の条件で2つのモデルを比較しました。それぞれのモデルで独立変数であるfim_in,age,mmse,paralysisから従属変数であるfim_outを予測しています。サンプル数を徐々に変えてサンプル数がそれぞれのモデルに与える影響を調べました。:
- 比較対象:重回帰分析、ランダムフォレスト(ハイパーパラメーターはデフォルト)
- 使用するデータ:前回と同じくFIMを模して機械的に生成したデータ。非線形性がある物を使用。データの分布は下のグラフのようになっています。
- 予測精度の評価指標:MSE(平均二乗誤差)- 予測値の大きなずれに敏感な指標
- サンプル数:50から始め、50ずつ増加させて800まで検証
- 各サンプルサイズで10回ずつモデル構築と評価を行い、MSEの平均値と標準偏差を記録しました。
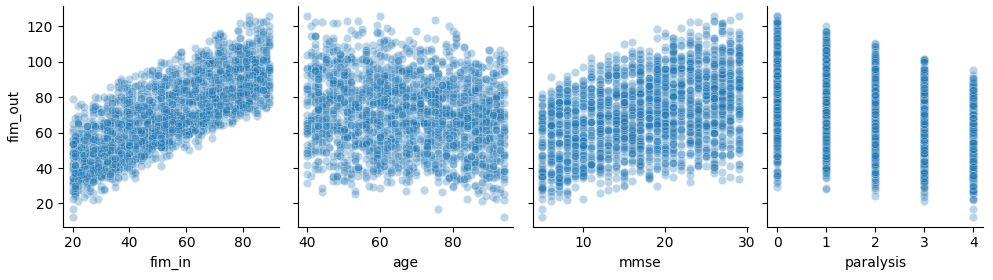
※ちなみに、線形データを使った場合は、ランダムフォレストと重回帰分析の精度にほとんど差が出ません。そのため今回は非線形データを使用しています。
線形・非線形データの区別についてはこちらの記事で解説しています。
⚠️ 注意:このデータは機械的に生成した架空の物です。実際の患者特性や臨床データを再現したものではありません。
結果と考察
結果の概要
以下のグラフはランダムフォレストと重回帰分析それぞれで予測したときの誤差を記録したグラフです。実線が誤差の平均値です。それぞれのサンプル数で10回ずつ予測を繰り返したときに、どれぐらい誤差にばらつきが出たかを色つきの帯で示しています。
例えばランダムフォレストを示す青色のグラフは、サンプル数50だと平均して80ぐらいの誤差があり100以上の誤差が出ることもあったという事が分かります。

以下の二つのグラフはSHAP値をプロットしたものです。上がフォレストプロットのSHAP値で下が回帰分析のSHAP値です。左右の位置がSHAP値の大きさ、色は説明変数自体の大きさを示しています。fim_inを見てみると、左右の広がりが変数の中で一番大きく、SHAP値が大きいものほど色が赤くなっています。これは変数の中ではfim_inがfim_outへの影響が一番大きく、fim_inが大きいほどfim_outも大きくなることを表しています。


グラフから読み取れる主なポイント:
- ランダムフォレストはサンプル数増加に伴い精度が向上
- サンプル数が少ない場合(〜200件)は重回帰分析の方が安定して良い結果
- サンプル数が中程度(200〜400件)になると徐々に精度が向上
- サンプル数400ぐらいで精度が逆転する。
- サンプル数が増える(700件~)と精度がはっきりと安定し、明確に回帰分析よりも良い制度を出すようになる。
- 推定精度のばらつき
- サンプル数が少ない場合、ランダムフォレストの推定結果は不安定
- 特に200件以下では過学習の影響が大きく、テストデータでの予測精度が安定しない
- SHAP値は大きく変わらない。
- 多少の差はあるものの、ランダムフォレストと回帰分析で結果が大きく変わることはなさそう。
結果から考えられること
サンプル数が少ない場合(〜200件)
ランダムフォレストはサンプル数が少ないと推定精度が低い傾向がありました。これは過学習(オーバーフィッティング)の影響と考えられます。デフォルト設定では各木が深く成長しすぎて、少数データの偶然のノイズまで学習してしまった可能性があります。
改善策としては:
- 木の最大深さを制限する
- 葉ノードに必要な最小サンプル数を増やす
- 木の数を調整する
こういったハイパーパラメータ調整によって、少数サンプルでの精度向上が期待できます。
サンプル数が多い場合(400件〜)
サンプル数が増えると、ランダムフォレストは安定して高い予測精度を示しました。特に外れ値を含むデータセットでは、その頑健性が発揮されやすいと考えられます。
解釈性の観点から
ランダムフォレストのSHAP値による可視化は、医療現場でのモデル採用において大きな利点です。回帰係数のように単純ではありませんが、各変数の影響を視覚的に把握でき、非線形な関係性も捉えられます。
モデル選択のための比較表
| 特性 | 重回帰分析 | ランダムフォレスト |
| 少数データ(〜200件)での精度 | ◎ | △ |
| 大量データ(400件〜)での精度 | △ | ◎ |
| 解釈のしやすさ | ◎ | ○ |
| 実装の手軽さ | ◎ | ○ |
| 非線形データへの対応 | × | ◎ |
| 計算コスト | ◎ | ○ |
| 外れ値への頑健性 | △ | ◎ |
実務的な選択ガイド
サンプル数による選択目安
- 〜200件: 重回帰分析がベスト。安定性と解釈性に優れる
- 200〜400件: 目的に応じて選択。解釈重視なら重回帰、精度重視ならランダムフォレスト
- 400件〜: ランダムフォレストが精度面で優位。SHAP値による解釈も可能
医療現場での実用性
重回帰分析には普及率の高さという大きな利点があります。ほとんどの統計ソフトに実装されており、誰でも簡単に実行できます。また、回帰係数という明快な数値が得られるため、結果の解釈や報告が容易です。
臨床現場で重要なのは、分析結果を共有・説明できることです。回帰分析を理解している医療従事者は多いですが、機械学習モデルに詳しい人材を見つけるのは容易ではありません。この点を考慮すると、少数〜中程度のサンプル数では、重回帰分析が実用的な選択と言えるでしょう。
まとめ
使うならどっち?
- データが少ない or 分析経験が浅い → 回帰分析が安心
- 多くの統計ソフトで標準実装されており、結果も解釈しやすい
- 周囲にも相談しやすい(回帰分析ならわかる人が多い)
- データ数が多い or 非線形な関係を疑っている → ランダムフォレストも選択肢に
- 特にSHAP値による説明力を活かせると強力
- 外れ値が多い状況では回帰分析よりも良い結果が出る可能性あり
医療データ分析では、モデルの精度だけでなく解釈可能性や実装の容易さも重要な判断材料です。自分の持つデータ量と分析目的に合わせて、適切なモデルを選択されることをお勧めします。
前回比較したディープラーニングについては、一般的にランダムフォレストよりもさらに多くのデータが必要になりますが、SHAP値による解釈が可能なランダムフォレストの方が医療現場では実用性が高いと考えられます。
実験に使用したコード(参考)
以下のコードが今回の実験で使用したものです。
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
import shap
import matplotlib.pyplot as plt
# データ生成
np.random.seed(42)
n = 2000
fim_in = np.random.randint(20, 90, n)
age = np.random.randint(40, 95, n)
mmse = np.random.randint(5, 30, n)
paralysis = np.random.randint(0, 5, n)
noise = np.random.normal(0, 5, n)
fim_out = (
fim_in * 3 +
30 * np.sin(mmse / 10) -
(age - 35) / 2 +
(30 - paralysis**2) / 4 +
mmse * (6 - paralysis) +
noise
)
fim_out = fim_out / (fim_out.max() / 126)
df = pd.DataFrame({
'fim_in': fim_in,
'age': age,
'mmse': mmse,
'paralysis': paralysis,
'fim_out': fim_out
})
# 特徴量と目的変数
features = ["fim_in", "age", "mmse", "paralysis"]
target = "fim_out"
sample_sizes = [50, 100, 150,200,250,300,350,400,450,500,550, 600,650,700,750,800]
num_iterations = 10
results_lr = []
results_rf = []
results_std_lr = []
results_std_rf = []
for size in sample_sizes:
mae_list_lr = []
mae_list_rf = []
for i in range(num_iterations):
sample_df = df.sample(n=size, random_state=i)
X = sample_df[features]
y = sample_df[target]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=i)
# 線形回帰モデル
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
model_lr = LinearRegression()
model_lr.fit(X_train_scaled, y_train)
y_pred_lr = model_lr.predict(X_test_scaled)
mae_lr = mean_squared_error(y_test, y_pred_lr)
mae_list_lr.append(mae_lr)
# ランダムフォレストモデル
model_rf = RandomForestRegressor(n_estimators=100, random_state=i)
model_rf.fit(X_train, y_train)
y_pred_rf = model_rf.predict(X_test)
mae_rf = mean_squared_error(y_test, y_pred_rf)
mae_list_rf.append(mae_rf)
# SHAP解析
if size == max(sample_sizes) and i == 0:
print("SHAP解析を実行中...")
explainer_rf = shap.Explainer(model_rf, X_train)
shap_values_rf = explainer_rf(X_test)
shap.summary_plot(shap_values_rf, X_test, plot_type="bar")
shap.summary_plot(shap_values_rf, X_test)
plt.title("Random Forest SHAP Feature Importance")
plt.show()
explainer_lr = shap.Explainer(model_lr, X_train_scaled)
shap_values_lr = explainer_lr(X_test_scaled)
shap.summary_plot(shap_values_lr, X_test_scaled, feature_names=features, plot_type="bar")
shap.summary_plot(shap_values_lr, X_test_scaled, feature_names=features)
plt.title("linear regression SHAP Feature Importance")
plt.show()
results_lr.append(np.mean(mae_list_lr))
results_rf.append(np.mean(mae_list_rf))
results_std_lr.append(np.std(mae_list_lr))
results_std_rf.append(np.std(mae_list_rf))
# 結果表示
print("サンプルサイズ:", sample_sizes)
print("線形回帰の平均MAE:", results_lr)
print("ランダムフォレストの平均MAE:", results_rf)
# MAE推移の可視化(平均のみ)
plt.plot(sample_sizes, results_lr, label="Linear Regression", marker="o")
plt.plot(sample_sizes, results_rf, label="Random Forest", marker="s")
plt.xlabel("Sample Size")
plt.ylabel("Mean squer Error")
plt.title("モデル性能の比較")
plt.legend()
plt.grid(True)
plt.show()
# MAEと標準偏差の推移(エラーバー付き)
plt.figure(figsize=(10, 6))
results_lr = np.array(results_lr)
results_rf = np.array(results_rf)
results_std_lr = np.array(results_std_lr)
results_std_rf = np.array(results_std_rf)
plt.plot(sample_sizes, results_rf, label="Random Forest", color="blue")
plt.fill_between(sample_sizes, results_rf - results_std_rf, results_rf + results_std_rf, color="blue", alpha=0.2)
plt.plot(sample_sizes, results_lr, label="Linear Regression", color="green")
plt.fill_between(sample_sizes, results_lr - results_std_lr, results_lr + results_std_lr, color="green", alpha=0.2)
plt.xlabel("Sample Size")
plt.ylabel("Mean squared Error (MAE)")
plt.title("Comparison of MSE vs. Sample Size\n(Random Forest vs. Linear Regression)")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()




コメント