〜ディープラーニングと重回帰分析の比較〜
データを活用して臨床予測や研究を行う際、手元にある「サンプル数」が分析結果にどれほど影響するのかは、誰しもが気になるテーマです。
特に最近注目されているディープラーニングは、
「大量のデータがなければ性能を発揮できない」
とよく言われますが、それがどの程度なのか、実感しづらいことも多いのではないでしょうか。
そこで今回は、サンプル数の違いが予測精度にどう影響するのかを、ディープラーニングと重回帰分析という2つの代表的な予測手法で比較してみました。実験結果からそれぞれの手法を使い分ける一つの目安を提案していきます。
実験の概要
今回は、非線形な関係性を持つ架空のデータを2000件生成し、それを使って予測モデルの性能を検証しました。
※ちなみに、線形データを使った場合は、重回帰分析とディープラーニングの精度にほとんど差が出ません。そのため今回は非線形データを使用しています。
非線形性に対する2手法の違いについてはこちらの記事で解説しています
線形・非線形データの区別についてはこちらの記事で解説しています。
主な特徴量(説明変数):
fim_in(運動機能の初期スコア)mmse(認知機能スコア)age(年齢)- paralysis(麻痺重症度)
これらの変数を用いて、退院時のFIMスコア(fim_out)を予測するという設定でモデルを構築しています。
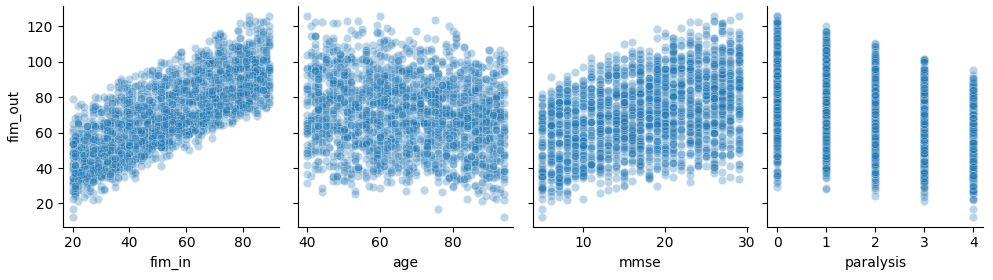
実際に使用したデータは以下のようなものです。特にMMSEとfim_outのグラフでデータの分布がカーブしており、グラフからも非線形性が確認できます。
⚠️ 注意:このデータは機械的に生成した架空の物です。実際の患者特性や臨床データを再現したものではありません。
使用した予測モデル:
- 重回帰分析(線形モデル)
- ディープラーニング(全結合ニューラルネットワーク:2つの中間層、各層16ニューロン)
サンプル数の変化と評価方法:
- 使用するサンプル数:50からスタートし、50刻みで800まで増加
- 各サンプル数で10回のモデル推定を実施
- 評価指標:MSE(平均二乗誤差)の平均値と標準偏差
これにより、「少ないデータ」「多いデータ」の場合に、それぞれのモデルがどのような挙動を示すのかを比較しました。MSEは予測値の大きなずれに対して敏感な評価指標です。
結果の概要と考察
結果のグラフ
以下のグラフはディープラーニングと重回帰分析それぞれで予測したときの誤差を記録したグラフです。実線が誤差の平均値です。それぞれのサンプル数で10回ずつ予測を繰り返したときに、どれぐらい誤差にばらつきが出たかを色つきの帯で示しています。
例えばディープラーニングを示す赤色のグラフは、サンプル数50だと平均して50ぐらいの誤差があり100以上の誤差が出ることもあったという事が分かります。
重回帰分析モデルの挙動:
- 平均的な誤差はサンプル数にあまり依存せず、一定の精度を保っている
→ サンプルが少ないと多少外すこともあるが、何度もやると予測はある程度の範囲に収まる - 推定精度のばらつき(標準偏差)はサンプル数が増えるほど減少
→ サンプルが増えると大きく外すことが減る - 少ないサンプルでもある程度の安定性を持ち、解釈もしやすい
ディープラーニングモデルの挙動:
- 少ないサンプル数では誤差が大きく不安定
→ サンプルが少ないと予測は「大外れ」か「結構外れ」のどちらかになりやすい - サンプル数が増えるに従い、急速に精度が向上
→ 予測の安定性も増し、大外れすることが減る - 今回使用したデータでは、サンプル数が200〜300件あたりで重回帰分析の精度を追い越す傾向
- ただし、500件程度まではばらつきが大きく、回帰分析の方が安定するケースもあり
- 1000件近くなると、予測精度はかなり安定し、明確に回帰分析より優位になる
💡 ディープラーニングモデルではサンプルが少ないと**「過学習」**が発生します。これは、少数のデータの偶然の揺らぎを「データ全体の特徴」と誤って学習してしまう現象です。
今回の実験でもこれが原因で、小サンプル時の推定精度が低下したと考えられます。
なお、グラフには出していませんが、データの非線形性(複雑さ)を増やすと、精度の逆転はもっと早く(サンプル数100ぐらい)起きることもありました。
まとめ:どちらを選ぶべきか?
サンプル数による比較
| サンプル数 | 推奨モデル | コメント |
|---|---|---|
| 〜200件 | 重回帰分析 | 精度・解釈性ともに優れる。DLは出番なし |
| 200〜500件 | 状況による | DLの精度が伸び始めるが、ばらつきに注意 |
| 500件〜 | ディープラーニング | 精度が安定し、回帰分析を明確に上回る傾向 |
目安としてはサンプル数200~300ぐらいが一つの境になりそうです。データの特性にもよりますが、これ以下であればディープラーニングを使う必要性はあまりないかもしれません。
逆にサンプル数が300以上あれば、ディープラーニングを検討する価値は十分ありそうです。
医療分野における使い分け
医療現場ではサンプル数が限られることが多いため、少数データでの予測には重回帰分析のようなシンプルなモデルが適していると言えます。
また、たとえデータが潤沢でも、FIM・MMSEなどのスコア予測のパイロット版としては、回帰係数を見ながら色々試せる重回帰分析の方が扱いやすい場合もあります。
一方で、電子カルテや大規模データベースの活用が進むにつれて、ディープラーニングの力を活かせる場面も今後ますます増えてくるはずです。
今後のモデル選定の参考になれば幸いです。
実験に使用したコード(参考)
以下のコードが今回の実験で使用したものです。
#■■■■■■■■■■■■FIMっぽいかんじのデータを生成■■■■■■■■■■■■■■■■■
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
# 再現性のためのシード
np.random.seed(42)
# データ数
n = 2000
# 特徴量を人工的に作成
fim_in = np.random.randint(20, 90, n)
age = np.random.randint(40, 95, n)
mmse = np.random.randint(5, 30, n)
paralysis = np.random.randint(0, 5, n) # 0=軽度, 1=中等度, 2=重度
# 非線形な退院時FIMの生成
# 例: sinやlogを含み、paralysisは非線形に影響
noise = np.random.normal(0, 5, n)
fim_out = (
fim_in*2 +
30 * np.sin(mmse/10) -
(age - 35)**2 / 100 +
(30 - paralysis**2)/4 +
mmse * (6 - paralysis) +
noise
)
fim_out = fim_out /(fim_out.max()/126)
# データフレーム化
df = pd.DataFrame({
'fim_in': fim_in,
'age': age,
'mmse': mmse,
'paralysis': paralysis,
'fim_out': fim_out
})
# 説明変数・目的変数に分ける
X = df[['fim_in', 'age', 'mmse', 'paralysis']]
y = df['fim_out']
# 訓練・テストに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
# ■■■■■■サンプル数を徐々に増やしながら10回ずつ推定。平均値と標準偏差を帯状に表示。■■■■■■■■■■
sample_sizes = [50, 100,150, 200,250, 300,350, 400,450, 500,550,600,650,700,750,800]
repeat = 10
mse_lr_all = {size: [] for size in sample_sizes}
mse_dl_all = {size: [] for size in sample_sizes}
features = ['fim_in', 'age', 'mmse', 'paralysis']
target = 'fim_out'
for size in sample_sizes:
print(size)
for i in range(repeat):
# サンプルサイズ分だけ取得(乱数シードを変えることで違うサンプルに)
df_sample = df.sample(n=size, random_state=i)
X = df_sample[features]
y = df_sample[target]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
# === 標準化 ===
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 線形回帰モデル
model_lr = LinearRegression()
model_lr.fit(X_train_scaled, y_train)
y_pred_lr = model_lr.predict(X_test_scaled)
mse_lr = mean_squared_error(y_test, y_pred_lr)
mse_lr_all[size].append(mse_lr)
# ディープラーニングモデル
model_dl = Sequential([
Dense(16, activation='relu', input_shape=(X_train_scaled.shape[1],)),
Dense(16, activation='relu'),
Dense(1)
])
model_dl.compile(optimizer=Adam(0.01), loss='mse')
model_dl.fit(X_train_scaled, y_train, epochs=100, verbose=0, batch_size=8)
y_pred_dl = model_dl.predict(X_test_scaled).flatten()
mse_dl = mean_squared_error(y_test, y_pred_dl)
mse_dl_all[size].append(mse_dl)
# 平均と標準偏差を計算
mse_lr_mean = [np.mean(mse_lr_all[size]) for size in sample_sizes]
mse_lr_std = [np.std(mse_lr_all[size]) for size in sample_sizes]
mse_dl_mean = [np.mean(mse_dl_all[size]) for size in sample_sizes]
mse_dl_std = [np.std(mse_dl_all[size]) for size in sample_sizes]
# グラフ描画
plt.figure(figsize=(12, 6))
plt.plot(sample_sizes, mse_lr_mean, label='Linear Regression MSE', color='blue')
plt.fill_between(sample_sizes,
np.array(mse_lr_mean) - np.array(mse_lr_std),
np.array(mse_lr_mean) + np.array(mse_lr_std),
color='blue', alpha=0.2)
plt.plot(sample_sizes, mse_dl_mean, label='Deep Learning MSE', color='red')
plt.fill_between(sample_sizes,
np.array(mse_dl_mean) - np.array(mse_dl_std),
np.array(mse_dl_mean) + np.array(mse_dl_std),
color='red', alpha=0.2)
plt.xlabel('Sample Size')
plt.ylabel('Mean Squared Error (MSE)')
plt.title('MSE vs Sample Size with Std Dev Bands (10 trials)')
plt.legend()
plt.grid(True)
plt.show()




コメント