はじめに
データサイエンスや統計学を勉強していると、**「なんだこの響き…?」**という独特な言葉に出会うことがあります。
「ポチョムキン理解」「マハラノビス距離」「バリマックス回転」…
一見すると難しそうですが、ちょっとした由来やイメージを知ると、意外と覚えやすいし勉強が楽しくなります。
今回は、響きがクセになるデータサイエンス用語5つを、雑学や実例を交えながらゆるく紹介します。
1. ポチョムキン理解|わかった気になってるだけの危うい状態
響きインパクト:★★★★★
意味のギャップ:★★★★☆(ロシアの偽村が由来!)
「ポチョムキン理解」というのは、わかったつもりになっているけれど、実際は理解できていない状態のこと。
由来はロシア帝国の伝説にある「ポチョムキン村」です。
女帝エカチェリーナ2世の視察のために、側近のポチョムキンが見栄えだけの偽の村を建てて誤魔化したという話からきています。

ChatGPT作
データサイエンスの世界でも、
- 「p値が0.05未満だから有意です!」と言いながら、
有意差の意味や前提条件を理解していない - とりあえず機械学習のライブラリを動かしただけで、
モデルの仕組みはまったく説明できない
こういうとき、まさにポチョムキン理解です。
用語ポイント
- 見かけだけ理解してるっぽいけど、中身がスカスカ
- 統計やAIは特に“ポチョムキン理解”に陥りやすい
ちょっと自戒の意味も込めて、覚えておきたい言葉ですね。
2. マハラノビス距離|多変量データの“真の距離”
響きインパクト:★★★★☆
使うと賢そう度:★★★★★
普通の距離(ユークリッド距離)は、単純に2点の直線距離を測るだけ。
でも多変量データでは、変数同士の相関や分散を考慮しないと本当の“近さ”はわからないんです。
そこで登場するのがマハラノビス距離。
共分散行列を使ってスケール調整し、多次元空間での距離をより正確に測る指標です。
ちょっとわかり隋と思うので、グラフを使って説明します。
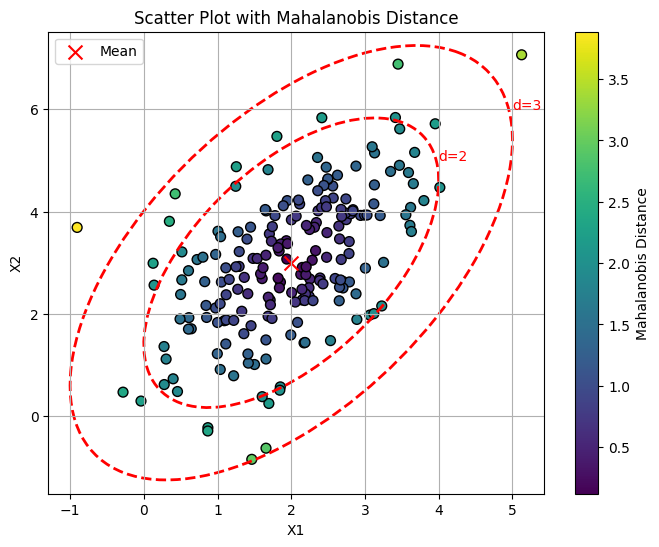
下のグラフを見ると、散布図が楕円の形になっています。このようなデータの分布になっているとき、平均値から左下(1,2)にずれたデータと右下(3,2)にずれたデータでは同じ距離でも意味合いが変わってきます。
左下にずれた場合はよくあるデータの一つという扱いになりますが、右下にずれた場合は他のデータの分布があまりなくまれな現象が起きたと考えることが出来ます。
このように、データの分布を考慮した平均値からの距離をマハラノビス距離と言います。
例えば、異常検知(外れ値検知)では
- 平均値からどのくらい離れているか
- その変数のばらつきを考慮して“どのくらい異常か”
を測るのにマハラノビス距離が使われます。
ちなみに名前の由来はインドの統計学者プラサンタ・チャンドラ・マハラノビス。
インドの大河のようなリズムの名前が、そのまま距離の名前になりました。
用語ポイント
- 多変量データの距離を測るときの“正しいものさし”
- 外れ値検知やクラス判別に大活躍
3. モンテカルロ・シミュレーション|確率で未来を読む
響きインパクト:★★★☆☆(でも華やか)
イメージしやすさ:★★★★★(カジノの街が由来)
モンテカルロ・シミュレーションは、
大量の乱数を使って、確率的に未来を予測する方法です。
- 株価やリスクのシナリオ分析
- 自然現象のシミュレーション
- AIのパラメータ探索
など、**「計算では解けない複雑な問題を、乱数で近似的に解く」**ときに使われます。
名前の由来は、カジノの街モンテカルロ。
サイコロやルーレット=確率の世界、というイメージから名付けられました。
用語ポイント
- サイコロを大量に振って確率的に未来を予測する
- 実は金融工学からAIまで幅広く活躍
華やかな名前なのに、意外と泥臭くランダムに計算するのが面白いところです。
4. バリマックス回転|因子分析をもっと見やすく
響きインパクト:★★★★☆(必殺技っぽい)
実はシンプル度:★★★☆☆
因子分析をすると、複数の因子にデータが複雑に関係していて**「この因子は何を意味してるの?」となりがちです。
そこで結果を“回転”させて、よりシンプルに解釈しやすくするのがバリマックス回転**。
バリマックス(Varimax)は、
- Variance(分散)
- Maximum(最大化)
を組み合わせた造語で、因子負荷量の分散を最大にして解釈しやすくする方法です。
心理学の調査データやマーケティング分析では定番のテクニック。
用語ポイント
- 因子分析の結果をスッキリ見せるための回転
- 名前がカッコいい割に、やることは“解釈を楽にする”地味な作業
5. カルマンフィルタ|ノイズをなめらかにする魔法
響きインパクト:★★★★☆(なんか強そう)
現代技術にめちゃ使われてる度:★★★★★
カルマンフィルタは、ノイズだらけのデータから本当の状態を推定するアルゴリズムです。
ちょっとしたテストをしてみました。
動画に出ているのは加速度計(mpu-6050)でx,y,z軸の加速度を取得することが出来ます。ただ、精度が高いものではないので、出力されるデータにはノイズが含まれます。動画のようにセンサーを動かして加速度データを取得します。
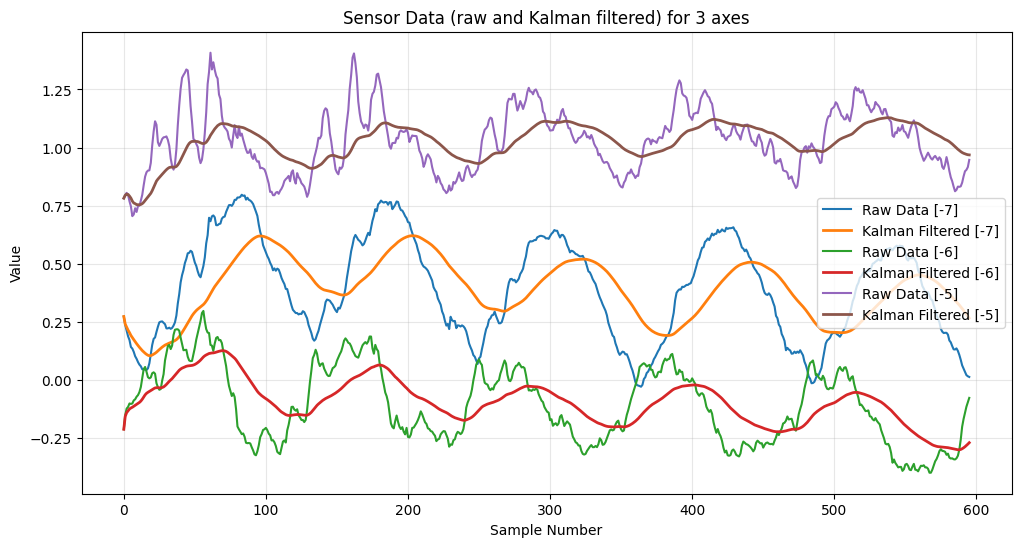
センサーの生データとカルマンフィルタで補正したデータを重ねたものが下のグラフです。
ノイズによりグラフがギザギザしていたのが、フィルタにより滑らかになっています。
実社会でもいろいろなところで使われており、例を挙げると以下のような使用例があります。
- 自動運転車がGPSやセンサーの誤差を補正するとき
- ロボットの位置推定
- 株価のトレンドや信号処理
名前の由来はハンガリーの数学者ルドルフ・カルマン。
“フィルタ”という名前ですが、単なるノイズ除去ではなく予測と補正を繰り返して滑らかな推定を行うのがポイントです。
用語ポイント
- ノイズがあるデータから真の状態を推定
- ロボット工学や金融でも超重要
さいごに|言葉の響きから入ると勉強がちょっと楽しい
データサイエンスの世界には、ポチョムキン理解・マハラノビス距離・カルマンフィルタ…
とにかく響きが面白い言葉がたくさんあります。
難しい理論も、名前の由来や雑学を知ると少し親しみが湧いて、勉強のとっかかりになることも。
おまけ:理学療法士の学生時代に衝撃を受けた言葉
実は私が理学療法士の学生だった頃、
一番インパクトを受けたのは**「解剖学的嗅ぎタバコ窩」**でした。
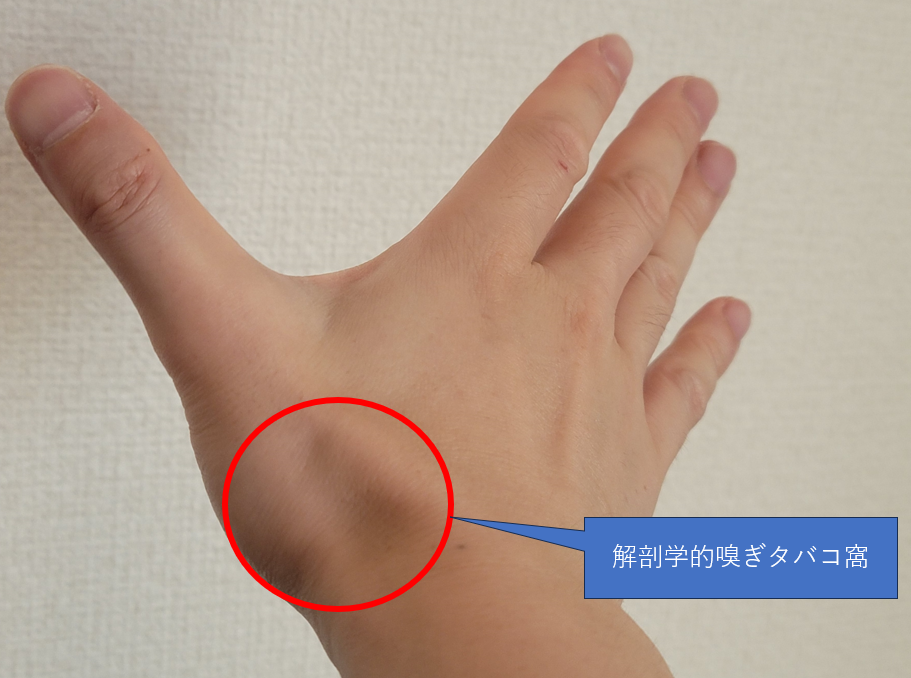
手の親指と人差し指の間のくぼみのことですが、
「こんなただのくぼみにまで名前がついてるのか!」と妙に記憶に残っています。
(昔のヨーロッパではそこにタバコの粉を詰めて嗅いでいたそうです…)
こういう言葉の響きや背景のストーリーって、勉強の楽しさを少し広げてくれるんですよね。




コメント