はじめに
この記事では、無料で使える統計ソフト JASP を利用した主成分分析のやり方を紹介します。主成分分析(Principal Component Analysis, PCA)は、変数間の相関や共分散を利用して、複数の変数を縮約し整理するための代表的な手法です。医療系の臨床研究や社会・心理学の分野で広く使われているだけでなく、近年では機械学習における前処理の一環としても活用されています。
主成分分析の主な用途は大きく三つに分けられます。
第一に「次元の縮約」であり、多くの変数をできるだけ情報を失わずに少数の成分にまとめることができます。これは回帰分析や機械学習の前処理としても有用です。
第二に「相関構造の把握」で、複数の変数がどのように関連しているかを整理することができます。
第三に「可視化」があり、多次元データを2次元や3次元の図に落とし込むことで、直感的に解釈しやすくなります。
なお、似た手法として因子分析があります。両者は「多数のデータから特徴を抽出する」という共通点を持っていますが、目的は異なります。主成分分析は複数のデータをコンパクトにまとめることを目的とするのに対し、因子分析は複数のデータの背後に潜む潜在因子を抽出することを目的としています。研究や分析の目的に応じて、適切な手法を選択することが大切です。
ここで紹介するのは、無料で使える統計ソフト JASP を用いたPCAの実行方法です。JASPは、マウスのクリック操作だけで統計解析ができるソフトであり、Excelのようにメニューを選んで進める感覚で使えます。難しいプログラミングは一切必要なく、RやPythonのようなコードを学ぶ必要もありません。そのため、統計ソフトに慣れていない方でもすぐに主成分分析を行うことができます。
本記事では操作画面のスクショを交えながら進めていきます。JASPでのPCA実行をキャプチャした60秒程度の動画も用意しましたので、最初にこちらをご覧いただくと全体の流れをつかみやすいでしょう。
データ準備
今回使用するデータ
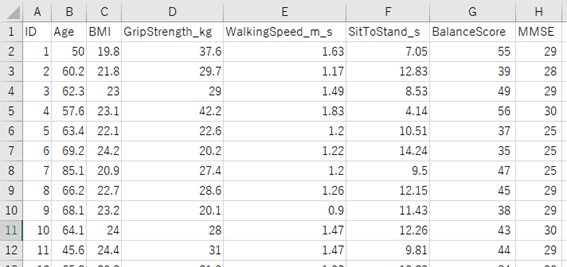
PCAを始める前に、まずはデータをJASPに読み込む必要があります。本記事では例として、臨床機能評価に関するサンプルデータを使います。
ID(対象者番号)
Age(年齢)
BMI(体格指数)
GripStrength(握力, kg)
WalkingSpeed(歩行速度, m/s)
SitToStand(立ち上がり時間, 秒)
BalanceScore(バランス評価)
MMSE(認知機能スコア)
これらは医療の現場でよく用いられる評価指標です。データの準備段階で一つ注意点があります。日本語の列名や特殊文字は文字化け・エラーの原因になります。半角英数で列名を記載するようにしましょう。
なお、今回使用するデータは統計ソフトで機械的に生成されたものです。実際の臨床象を反映したものではありません。ご注意ください。
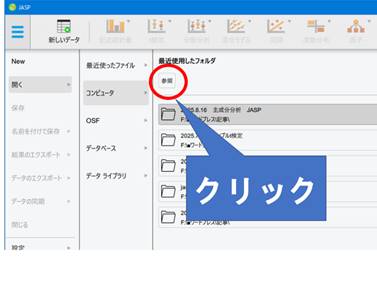
JASPでのデータ読み込み手順
- JASPを起動し、左上の File メニューから開く→コンピュータ→参照を選びます。

- 保存してあるCSVファイルを指定すると、JASPのデータビュー画面に表形式でデータが読み込まれます。
- データ確認のポイント
読み込んだ直後には、次の点を簡単に確認しておきましょう。
- 変数名 が正しく表示されているか
- 欠損値(空欄)がないか
- すべての解析対象変数が数値データになっているか
とくにPCAは数値データを前提とした手法なので、文字列データ(例:男/女、あり/なしなど)が混ざっていないか注意が必要です。このようなデータは(男性/女性→1/0)のようなダミーデータに置き換える必要があります。
PCAの実行(JASPでの手順)
データが問題なく読み込めたら、いよいよ主成分分析を実行します。JASPではマウス操作だけで設定できるため、プログラミングの知識は不要です。画面上部のメニューから因子→主成分分析とクリックしてください。
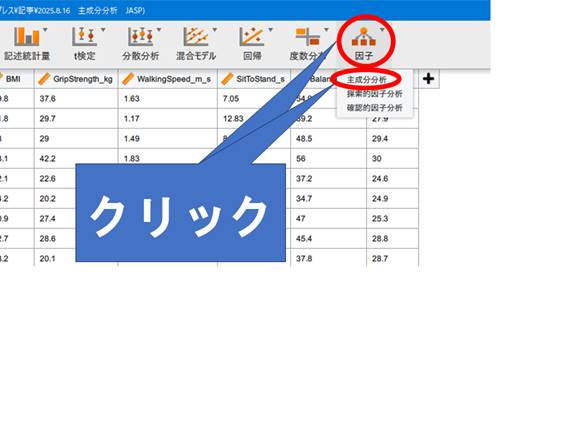
変数の選択
解析に使う変数を指定します。左の枠にある変数群から使用するものを選択し、右側の変数欄にドラッグ&ドロップで移動します。
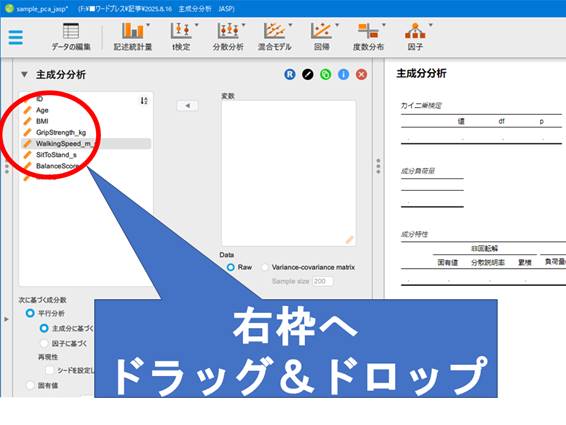
変数枠へ項目を移動するとすぐに解析結果が右の出力ウィンドウに出てきます。
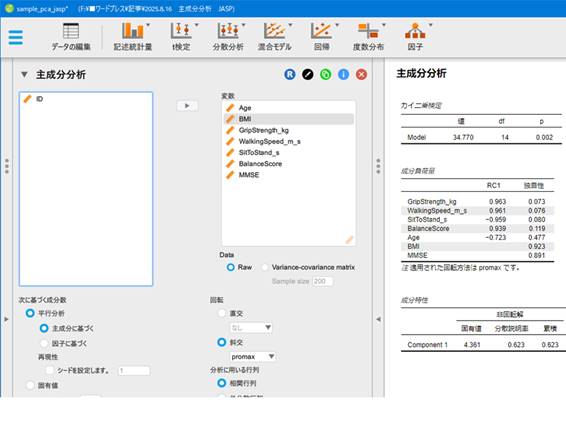
分析設定のポイント
今回の分析では以下のオプションを指定しています。
- 次に基づく成分数→手動 成分数:2
- KMO検定
- Bartlettの検定
- 平行分析(平行分析の結果を見る場合にチェックします)
- パス図
- スクリープロット
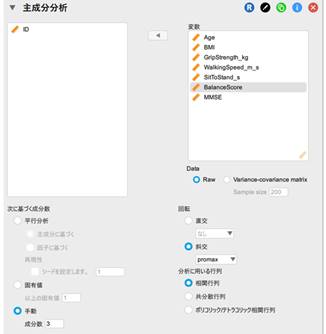

「分析に用いる行列の項目」ですが、ざっくりとした選択基準は以下のようになります。
- 相関行列:データの単位による数値の大きさを無視して公平に扱いたい時(身長、体重、筋力で解析など)
- 共分散行列:家計における項目ごとの金額のように、項目間の数値の大小の影響を残したい時(食費、交際費、通信費など)
- ポリコリック/テトラコリック相関行列:順序尺度の解析の時
解析はこれで完了です。
右の出力ウィンドウに以下のような解析結果が表示されます。
これらの結果をどう読み解くかは、次の章「結果の解釈」で解説します。
結果の解釈
JASPでPCAを実行すると、固有値や寄与率、主成分負荷量、散布図などの結果が表示されます。ここでは、各出力の見方と解釈方法を説明します。
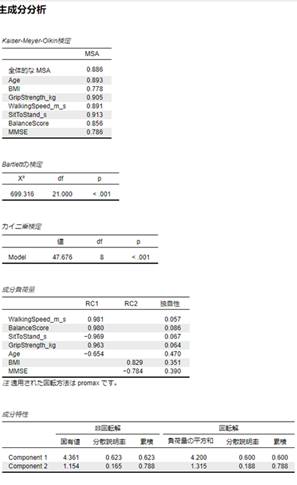
PCAの前提条件の確認(KMO・Bartlett検定)
JASPではKMO・bartlett検定のオプションが用意されています。PCAは変数間の相関を前提としており、相関がほとんどない場合は意味のある主成分を抽出できません。その確認に使えるのが、 Kaiser-Meyer-Olkin(KMO)検定 と Bartlettの球面性検定 です。
KMO検定とは
KMO検定は、各変数が他の変数とどれだけ相関しているかを評価する指標です。値の目安は次の通りです。
- 0.8以上:非常に適している
- 0.7前後:適している
- 0.6未満:PCAには不十分
KMOの値が高いほど、PCAによる次元縮約が有効であると判断できます。
Bartlettの球面性検定とは
Bartlettの検定は、変数間の相関がほとんどない(=単位行列である)という帰無仮説を検証します。
- p < 0.05 であれば、変数間に十分な相関があると判断でき、PCAを適用可能です。
出力結果の例
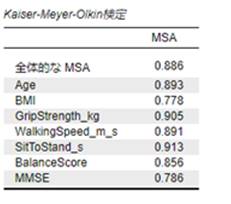
今回の例では、すべての変数で0.7を上回っているため、KMO検定から主成分分析に適したデータであることが分かります。
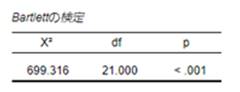
Bartlettの検定でもp<0.05であり、変数間の相関が無いことが否定されるため、主成分分析に適したデータであることが示されています。
必要な場合は、こういった検定を使用して、データが主成分分析に適しているか判断しましょう。
固有値と寄与率
固有値は主成分がどれだけの情報(分散)を説明しているかを示す指標で、寄与率(分散説明率)はそれを割合で示したものです。例えば今回のサンプルでは以下の通りです。
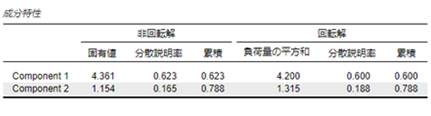
- 累積:0.788
主成分数の決定(後述)に関して累積寄与率を判断の基準にする場合、一般に累積寄与率0.7~0.8以上が一つの目安となります。今回の例では、主成分二つで累積(累積寄与率)が0.788となり、0.7を超えるため、データの大部分を集約できていると判断できます。このため、主成分数は二つが妥当と判断します。
累積寄与率により主成分数を決定する場合は、この表を見ながら検討するのが良いでしょう。
各成分の固有値を使用して主成分数を決定することもできます。その場合は「固有値 以上の固有値」にチェックを入れると、指定の値以上の固有値を持つ主成分を出力してくれます。
主成分数の決め方
主成分としていくつの成分を抽出するかは、解析者が主成分分析の用途や結果を考慮して決めます。目的に応じて複数の決め方があり、以下のような方法と特徴があります。
累積寄与率
- 判断方法:累積寄与率が 70〜80%以上を目安に、データの特徴を主成分として十分抽出できていると判断する。
- 適した用途:情報を一定割合保持したい場合。特に機械学習・パターン認識・画像処理などで「どこまで情報を残すか」を明確にしたいとき。
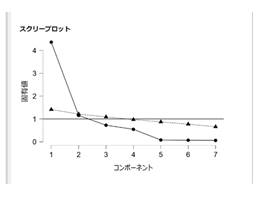
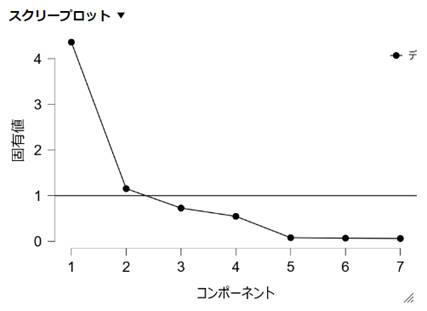
スクリープロット
- 判断方法:固有値を大きい順に並べてグラフ化し、折れ曲がり(エルボー)の位置で打ち切る。グラフがなだらかになるひとつ前までの主成分を残すことが多いようです。このグラフでは、コンポーネント2あたりからなだらかになっている為、その前の主成分1(コンポーネント1)のみを残すという判断になります。
- 適した用途:探索的な分析に適する。心理学・社会学などで、データの背後にある因子数を直感的に把握したいとき。
固有値1以上の基準(カイザー基準)
- 判断方法:標準化データの場合、固有値が1以上の主成分を残す。
- 適した用途:心理測定・教育測定などの古典的な研究で補助的に利用。近年は残しすぎる傾向があるため、他の基準と併用されることが多い。
平行分析
- 判断方法:ランダムデータから得られた固有値と比較し、実データの固有値が大きい主成分だけを残す。
- 適した用途:心理学・社会科学などで因子数を決める標準的な方法。信頼性が高く、探索的因子分析でもよく用いられる。
※平行分析による主成分数決定をする場合は、「次に基づく成分数」の「平行分析」にチェックを入れます。平行分析の結果を確認したい場合は、出力オプションの「平行分析」にチェックを入れてください。
手動で指定
- 判断方法:分析目的に応じて主成分数をあらかじめ決める。
- 適した用途:
- 回帰分析の前処理(次元削減) → サンプルサイズに応じて項目数を制約。累積寄与率も考慮して総合的に判断。
- 可視化(2D・3Dプロット) → 2〜3主成分に限定して図示。
- 実用目的で「解釈のしやすさ」や「扱いやすさ」を優先する場合。
主成分の意味付け
主成分の意味付けはソフトが自動で行ってくれるものではなく、解析者自身が変数の特性や背景を踏まえて判断する必要があります。負荷量やパス図(後述)を確認してパターンを把握し、抽出された主成分にどのような意味付けをするか考えます。
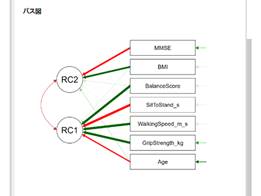
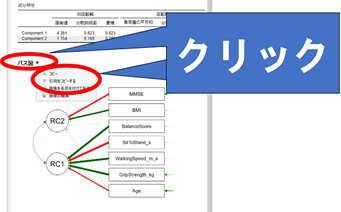
なお、設定エリアでプロットの「パス図」にチェックを入れると以下のようなグラフを出力できます。
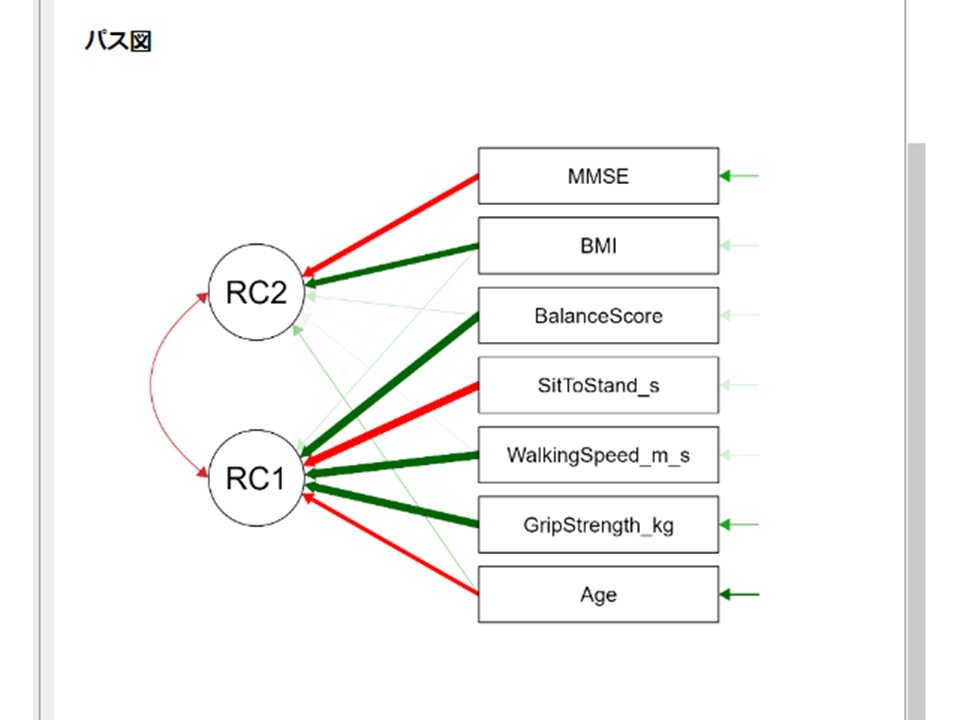
負荷量や関連の正負が矢印の色と太さで表現され、関係性を視覚的に把握できます。
RC1を見てみると、BalanceScore~Ageまで五つの項目で合成されており、矢印の色からSitToStandとAgeは負の相関であり、矢印の太さからAgeは主成分への影響が小さいことが分かります。
また、運動機能の項目がRC1に集約され、その他の項目がRC2に集まっています。最終的な目的が紙面でのグラフ化などであればこのままでもいいかもしれません。しかし、解釈性を優先するのであれば、主成分を3つに増やして、運動成分・認知成分・体格成分と分けた方が理解しやすいでしょう。
結果の外部出力
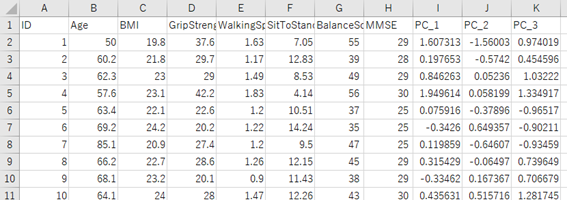
主成分得点の出力
主成分分析によりデータを縮約したスコア(主成分得点)は外部出力することができます。主成分分析を回帰分析の前処理として行ったり、多次元データをまとめてグラフに図示したりする場合はこの手順が必要です。
設定エリアの下の方にある出力オプションから「データに成分スコアを追加」にチェックを入れます。
次にメインメニューの「三」のマークから「データのエクスポート」→「コンピューター」→「参照」と選択し、好みのフォルダに保存してください。
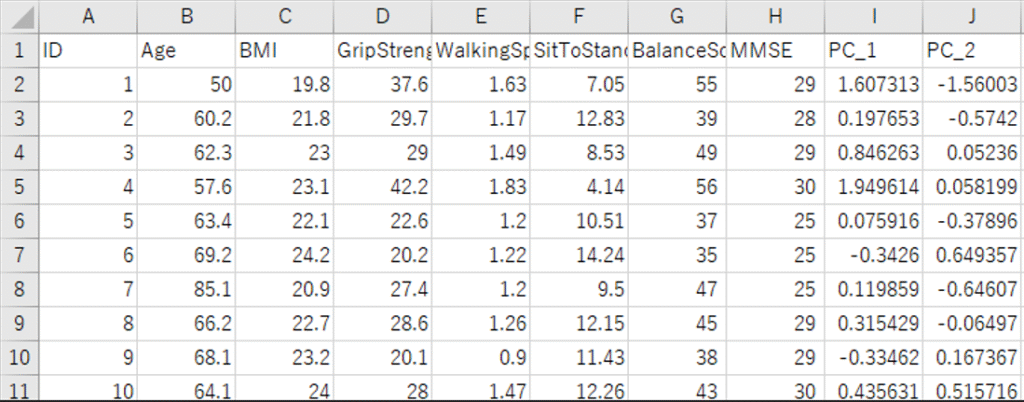
保存されたファイルを開くと、以下のようにもとのデータに主成分得点列が追加されているのが確認できます。
グラフを保存する場合:
表やグラフを保存することもできます。
グラフの場合は、グラフタイトルをクリックしてメニューを出します。そこから「コピー」をクリックしてWordやPowerPointなどのソフトに貼り付けるか、「画像を名前を付けて保存」をクリックして好きなフォルダに保存しましょう。
表を保存する場合:
こちらもグラフと同様です。表のタイトルをクリックするとメニューが表示されます。「コピー」を選んで、WordやPowerPointなどのソフトに貼り付けてください。貼り付けた後は編集することもできます。
まとめ
本記事では、JASPを用いた主成分分析(PCA)の手順と結果の読み解き方について解説しました。
PCAの目的
- 主成分スコアを使えば、クラスタ分析や回帰分析の入力変数として活用可能です。
- 多次元データを2次元や3次元に縮約できるため、視覚的な理解にも有効です。
PCAを使うときの前提
- 変数間にある程度の相関がある場合に適用可能
→ 相関が全くない変数はまとめても意味がありません。
結果の解釈で気をつけたい点
- 主成分分析を行う目的に応じて、主成分数の決定方法を選びます。
なお、累積寄与率が低すぎるような場合は、変数の選択や方法を再検討しましょう。 - 主成分に与える「意味づけ」は解析者自身の判断
→ JASPは数値を出すだけで、解釈は自分で行う必要があります。




コメント