はじめに
医学論文や学会発表を見ていると、ほとんどの研究で「p < 0.05」「有意差あり」という言葉を目にします。
しかし、その「p値」が何を意味しているのかを、正確に説明できる人は意外と多くありません。
「p値が小さい=効果がある」「p値が大きい=効果がない」——
そんな単純な理解のまま結果を解釈してしまうと、研究の本質を見誤ることがあります。
近年では、米国統計学会(ASA)をはじめ世界的に「p値だけに頼らない統計解釈」が重視されるようになり、効果量(Effect Size)や信頼区間(Confidence Interval)、そして臨床的に意味のある最小の変化量(MCID)といった新しい視点が求められています。
この記事では、「p値とは何か」から始めて、その限界や注意点、そして今後の研究で大切にすべき統計的視点を、医療従事者にも分かりやすく解説します。
論文を“読むだけ”でなく、“理解して活かせる”ようになるための第一歩として、p値の本当の意味を一緒に整理していきましょう。
「p値」ってそもそも何?
医学論文や研究発表でよく出てくる「p値(p-value)」という言葉。
一見すると難しそうですが、簡単に言えば「もし本当は差がないとしたら、今回のような結果が偶然に出る確率」のことです。
たとえば、リハビリ介入AとBを比べて、p = 0.03 だったとします。
これは「実際には効果に差がないのに、たまたま3%の確率でこのくらいの差が出たかもしれない」という意味です。
p値が小さいほど“偶然とは思いにくい”結果というわけです。
そして、p値が0.05を下回れば「有意差あり」、つまり「介入の効果があった」と判断する——
このような読み方は長い間、医療統計の“常識”のように扱われてきました。
しかし近年、この“p値中心主義”に対して見直しの動きが世界中で進んでいます。
米国統計学会(ASA)をはじめ、多くの学会や主要ジャーナル(Nature、Science、JAMAなど)が、
「p値だけで結論を出さない」ことを推奨する声明を出しています。
本記事では、こうした医療統計の流れを整理しながら、
これから論文やデータを読むときに意識しておきたいポイントを、やさしく解説していきます。
「p < 0.05」の由来と注意点
多くの研究で「p < 0.05なら有意差あり」と書かれています。
これは「偶然でこうなる確率が5%未満だから、効果があると考えよう」という目安です。
でも、この“0.05”という数字に特別な根拠はありません。
統計学者ロナルド・フィッシャー(R.A. Fisher)が1920年代に「一つの目安」として提案したに過ぎません。
フィッシャー自身も「絶対に0.05で線を引け」と言ったわけではなく、あくまで“判断の参考”として提示したのです。
それが今では、「p < 0.05なら成功、そうでなければ失敗」といった風潮になり、結果を二分する基準のように扱われてしまいました。
しかしこれは、統計の本来の考え方とは少しズレています。
よく考えてみると、p値が 0.049なら「効果あり」、0.051なら「効果なし」 と判断するのは、少し不思議な話です。
実際にはこの2つの結果に大きな違いはなく、数字がほんの少し違うだけで結論が変わってしまうのは、やや極端とも言えます。
だからこそ最近では、「p値だけで判断しない」「効果量や信頼区間も併せてみる」という考え方が重視されるようになってきています。
p値の「落とし穴」
p値が小さいからといって、必ずしも「効果が大きい」とは限りません。
また、p値が大きいからといって「効果がない」わけでもありません。
なぜなら、p値は「偶然の可能性」を表すものであって、「どのくらい差があるのか」までは教えてくれないからです。
たとえば、1000人を対象にした大規模研究なら、ほんのわずかな差でもp < 0.05になります。
逆に、対象が20人しかいない小さな研究では、実際に大きな差があってもp > 0.05になってしまうこともあります。
つまり、p値だけで結論を出すと、本当の意味での“効果”を見誤ることがあるのです。
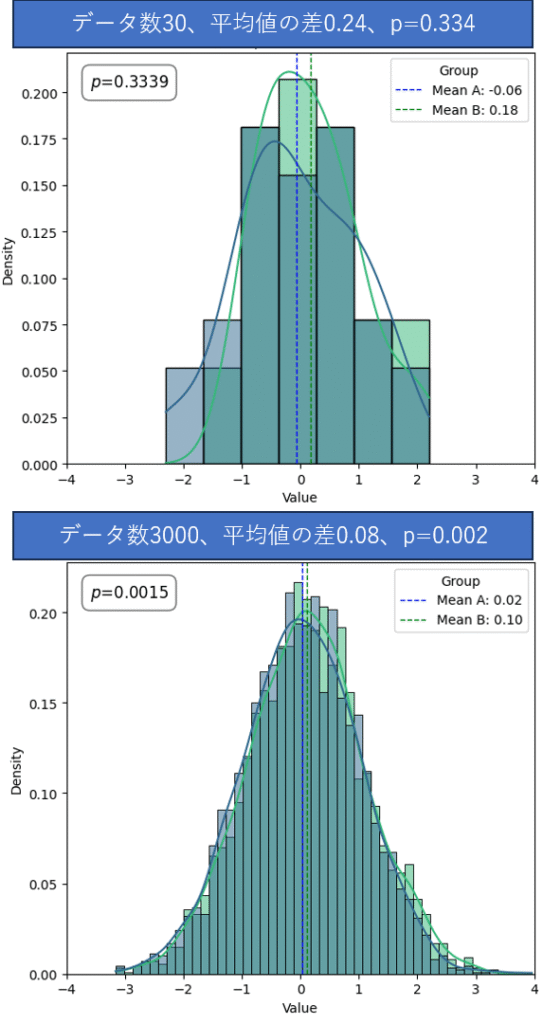
この図は、効果量(平均値の差)がほとんど同じでも、サンプルサイズが異なるとp値が大きく変わる例を示しています。それぞれサンプルデータを使用して、2群を比較しp値を計算しています。
上のグラフ(各群30名)ではp = 0.334で有意差なし。
しかし下のグラフ(各群3000名)では、平均の差は上より小さいにもかかわらずp = 0.002と有意差が出ています。
つまり、大規模研究ではわずかな差でもp値が小さくなりやすく、逆に小規模研究では大きな差でもp値が有意にならないことがあるのです。
「効果量」― 差の大きさを表す指標
ここで重要になるのが「効果量(Effect Size)」という考え方です。
効果量とは、「どのくらいの差があるのか」を数値で示したものです。
代表的なものに、Cohen’s d(平均値の差を標準偏差で割ったもの)やrなどがあります。
たとえば、介入AとBの平均差がわずかでも、サンプル数が多ければp値は小さくなります。
しかし、効果量を見れば「差が小さい」ことがすぐにわかります。
つまり、効果量は「統計的に有意」ではなく「実際に意味のある差かどうか」を考えるための指標なのです。
一般的には、
- d = 0.2 → 小さい効果
- d = 0.5 → 中くらいの効果
- d = 0.8 → 大きい効果
とされています。
効果量を見ることで、「有意差があった」としてもそれが“ほんのわずかな違い”なのか、“臨床的に重要な違い”なのかを判断できるようになります。
「信頼区間」― 結果の確かさを示す範囲
もう一つの大切な考え方が「信頼区間(Confidence Interval)」です。
信頼区間は、「真の値がおそらくこの範囲にあるだろう」という推定の“ゆらぎ”を示します。
たとえば、リハビリ介入Aの効果量が0.5で、95%信頼区間が「0.1~0.9」だったとします。
これは「実際の効果量は0.1から0.9の間にある可能性が高い」という意味です※。
もしこの区間が広い場合は、推定があいまいで信頼性が低いと考えられます。
逆に、狭い区間なら推定が安定していることを示します。
また、信頼区間に「0(差がない)」が含まれている場合は、統計的に有意とは言えません。
このように信頼区間を見ると、「結果がどの程度確からしいか」「どれくらい誤差を含んでいるか」が直感的に分かります。
※この表現は統計に詳しい方だとやや引っかかるかもしれません。しかし、統計を学ぶのが初めてであればこのような理解でもいいと思います。興味が出たら詳しく調べてみましょう。
「MCID」― 臨床的に意味のある最小の変化
さらに近年注目されているのが「MCID(Minimal Clinically Important Difference)」です。
これは「患者さんが実際に“良くなった”と感じるための最小限の変化量」を意味します。
たとえば、ある評価スケールで平均スコアが1点上がっても、本人が「変わった」と感じなければ、それは臨床的にはあまり意味がないかもしれません。
逆に、0.5点の改善でも、歩行や日常動作が明らかに楽になるなら、それは臨床的に大きな意味があります。
MCIDは、過去の調査や患者の自己評価から決められますが、リハビリ分野ではまだ十分に研究されていない項目も多いのが現状です。
それでも、今後は「p値が小さいから有効」ではなく、「MCIDを超える変化があったか」という視点も重要になるでしょう。
これからの研究の読み方
最近では、世界的にも「p値だけで結果を判断しない」流れが強まっています。
有名な医学雑誌(BMJ、JAMAなど)でも、研究報告にはp値だけでなく効果量や信頼区間を併せて記載することが推奨されています。
研究結果を読むときには、次の3点をセットで見ると理解が深まります。
| 指標 | 意味 | 確認ポイント |
| p値 | 結果が偶然に出た可能性 | 小さいほど偶然の可能性が低い |
| 効果量 | 差の大きさ | 数値が大きいほど実際の差が大きい |
| 信頼区間 | 結果の確かさ(推定精度) | 範囲が狭いほど推定が安定している |
| MCID | 患者が実感する最小の変化 | 超えていれば臨床的に意味がある |
なお、p値・効果量・信頼区間は文献の著者が書くものですが、MCIDは必ずしも掲載されていません。自分が良く対応する疾患の主要な評価項目に関しては、自分で調べてMCIDがどの程度なのか知っておく必要があります。
まとめ
p値は「偶然の可能性」を教えてくれる便利な指標ですが、それだけで“効果があるかどうか”を判断するのは危険です。
今求められているのは、p値だけでなく、効果量・信頼区間・MCIDといった多面的な視点でデータを読み解く力です。
研究結果を正しく読むには、
- 「どのくらいの差があり(効果量)」
- 「どの程度確からしく(信頼区間)」
- 「患者にとって意味があるか(MCID)」
という3つの視点を持つことが大切です。
この3つを意識して読むことで、論文の内容がぐっと理解しやすくなり、臨床にもより活かしやすくなるはずです。
統計は単なる数字の比較ではなく、「変化の意味」を見極めるためのツールです。
研究を読み解くときも、自分で研究を行うときも、p値の大小に縛られず、**“現場で本当に意味のある変化”**に目を向ける姿勢が大切です。
もう少し知りたい方は
統計に関する用語は難しく感じる事が多いですね。
こちらの記事ではt検定の場合を例に効果量や95%信頼区間について紹介しています。
もう少し調べてみたい方は合わせてご覧ください。




コメント