はじめに
「t検定って聞いたことあるけど、実際には何をしているの?」
そんな疑問を持つ方のために、この記事では t検定の考え方、p値の意味、自由度、効果量、信頼区間 など、統計的検定の読み解きに必要な基礎知識をわかりやすく紹介します。
t検定は医療・教育・心理などの現場でよく使われる統計手法です。
JASPなどの統計ソフトを使えばすぐに結果は出ます。しかし、単に数字を出すだけでは、それが何を意味し、あなたの問いにどう答えているのかはわかりません。結果があらわすものを理解することは、単なる計算結果の羅列を、意味のある「考察」へと変える鍵なのです。
「統計は苦手…」「難しそうで避けがち…」そう思っていませんか?ご安心ください。この記事では、t検定の考え方から、p値の意味、自由度、効果量、信頼区間といった基礎知識まで、グラフや具体例を交えながらわかりやすく解説します。t検定の「なぜ」を理解し、データ分析の自信を手に入れましょう。
「先にt検定のやり方を確認したい」という方はこちらで紹介しています。
【たった30秒】初心者でもできる!JASPでt検定+効果量+95%CI+グラフ作成!(関連2群)
【たった30秒】初心者でもできる!JASPでt検定+効果量+95%CI+グラフ作成!(独立2群)
対応のあるt検定・対応のないt検定の違いが気になる方はこちらの記事をご覧ください。
【初心者向け】t検定の種類と使い分けをやさしく解説!
t検定とはどんなもの?
t検定とは、2つのグループの「平均値に差があるかどうか」を判断する方法です。
たとえば…
- 新しい薬を投与したグループとしなかったグループで、血圧の平均に差があるか
- 男性と女性で、筋トレ後の筋肉痛の強さに違いがあるか
といった「2群の平均の差」が偶然か、それとも意味のある差かを統計的に判定します。
◎重要な考え方
差があるように見えても、それが偶然のブレの範囲内かもしれない。
t検定では、2つのグループのデータのバラつき(分散)に対して、群間の平均の差がどれくらい大きいかを見て判断します。
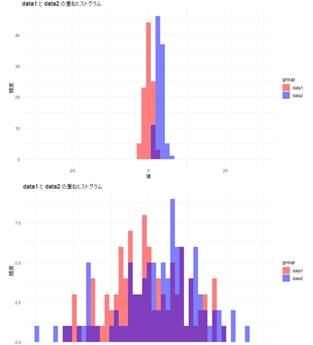
文字だけだとわかりにくいので、下の二つのグラフを見てみましょう。赤グループのデータと青グループのデータがグラフ上に表示されています。重なっている部分は紫になっています。
上のグラフでは青のデータと赤のデータはそれぞれ狭い範囲に集中しており、ばらつきが少ないです。これならパッと見て、赤グループと青グループには何か質的な違いがあると言えそうです。
一方、下のグラフではどうでしょう?ばらつきが大きくかなりの部分が重なっています。これでは平均値にずれがあるかどうかすぐに判断できません。仮に平均値を計算した結果ずれがあったとして、その差はデータのばらつきによる偶然でしょうか?偶然ではないのでしょうか?
これもすぐに判断するのは難しいと思います。
この判断を統計の力で行うのがt検定です。
p値とは何を表すもの?
p値とは、「もし2つのグループが、もともと全く同じような性質の集団だったと仮定したときに、偶然で平均の差が出てしまう確率」のことです。
これも文字だと理解しにくいので、グラフを見てみましょう。
ある患者群を二つに分けて、何もせずに検査をした赤グループと治療を行った青グループをグラフにしたと思ってください。
上で置いた仮定から「どちらのグループにも差は無く、似たような結果になる」と考えます。
この前提でグラフを見た時、たまたま下のようなグラフが得られる確率はどの程度でしょうか?
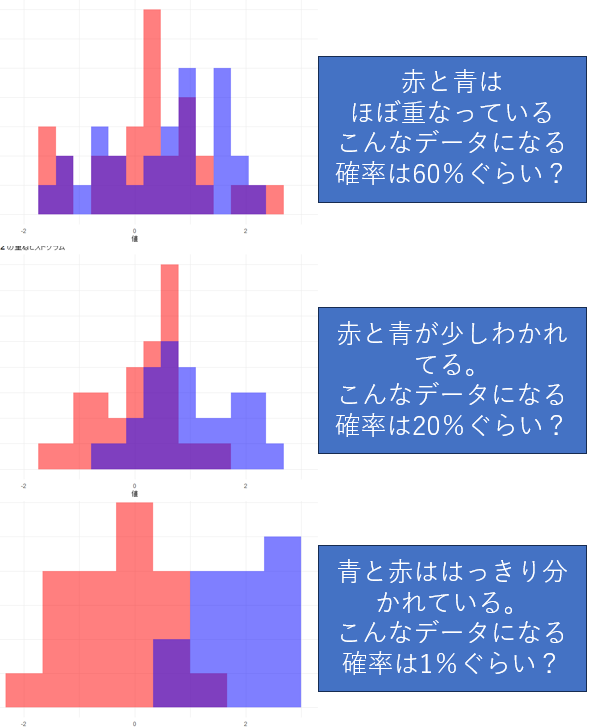
上のグラフは青と赤がほぼ重なっており、差がないのであればこんなデータだろうというグラフです。
真ん中のグラフはややずれがあります。同じような患者群でもたまたまデータが偏って、たまにはこうなるかな?というグラフです。
一番下のグラフでは赤グループと青グループがかなりはっきり分かれています。青・赤グループ間に差が無ければここまではっきり分かれる確率はかなり低いでしょう。このようなケースでは「同じような分布になるはずが、これだけデータがずれてしまうのはおかしい」と考えます。はじめにした仮定である「二つの群には差がない」を撤回して、「治療には効果が有りデータに差が生じたと判断」します。
ここでは説明のため、上のようなグラフになる確率を適当に決めました。実際は人間がデータを見て正確に確率を計算するのは大変です。この確率を統計的な手法で計算したものがp値です。
有意差があるとはどういうこと?
「有意差がある」とは、その差が偶然ではなく意味のある差だと判断したということです。一般にp値が0.05を下回ると、「意味が有った」と考えます。この閾値を有意水準と言います。
上の例で言えばp値が0.05を下回れば「青グループに施された治療には意味があった=効果が有った」と考えます。
なお、慣習的に有意水準は0.05とする事が多いですが、0.05という数字に根拠があるわけではありません。そのため研究の種類によっては0.01だったり0.1だったりすることもあります。
自由度ってなに?
自由度(degrees of freedom)とは、「データが持っている情報量」のようなものです。
計算の基本
t検定の自由度は、以下のように求められます:
- 対応のない2群のt検定(独立t検定):
自由度 = n₁ + n₂ − 2 - 対応のあるt検定(対応t検定):
自由度 = n − 1
なぜ重要なのか?
t検定はではt分布という確率分布を使用して、検定を行います。検定のときはt値という数値を計算し、自由度に応じたt分布に当てはめてp値を出すことになります。
t分布は自由度によって形が変わるため、同じt値でも自由度が違えばp値も変わります。
- 自由度が小さい → 分布の裾が厚く、厳しい判定になる
- 自由度が大きい → 正規分布に近づく(n ≧ 30 くらいで)
つまり、「自由度によって同じt値でも意味が変わる」ので、検定の結果を正しく解釈するには正しい自由度が必要となります。
また、rという効果量の指標を計算する時にはt値と自由度を使用して計算します。
効果量とは?p値との違いは?
効果量(effect size)とは、「差の大きさ」を示す指標です。
- p値:差があるのか?を表す
- 効果量:その差はどれぐらいか?表す
データのバラつき具合が異なると効果量は変わってきます。効果量はデータのばらつきと平均値の差で計算される相対的な指標です。
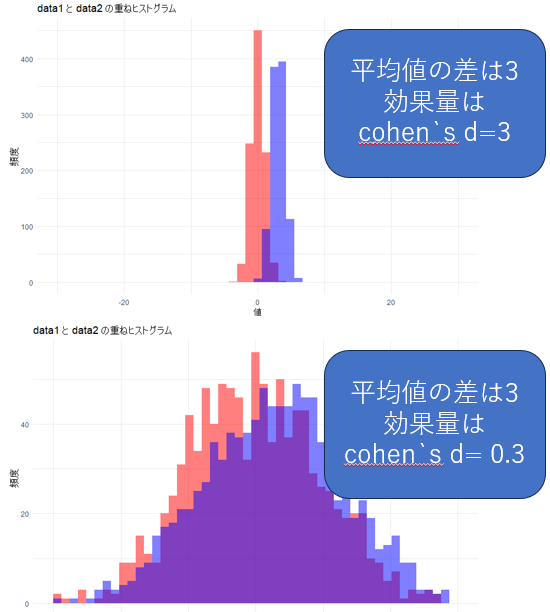
これもグラフを見てみましょう。どちらも平均値の差は同じですが、効果量を計算すると違いがあります。下のグラフではデータのばらつきが大きいため、相対的に効果量が低くなっています。
これは論文を読む時も同じです。似たような介入の文献でも、患者群のばらつきが大きければ効果量は低くなります。
例えば、回復期病棟で50回の立ち上がり動作練習をした時の下肢筋力の改善度合いを調べるとします。整形外科症例のみの研究と整形疾患・脳血管疾患・廃用症例をを全て含めた研究では効果量にも差が出る可能性が高くなります。整形外科のみの方が患者特性が均一なため、効果量が大きくなりやすいと言えます。
参考(Cohen’s d)
- 0.2:小さい効果
- 0.5:中くらいの効果
- 0.8:大きな効果
95%信頼区間(95%CI)とは?推定値を「幅」でみる考え方
t検定や効果量の結果には、よく「95%信頼区間(95%CI / 95% Confidence Interval)」という項目が表示されます。これは、“この範囲なら95%の確率で真の値を捉えられる”という推定の幅を表しています。
平均値や効果量は「サンプルからの推定値」
t検定で使う平均値の差や効果量などの数値は、あくまでサンプルから計算された“推定値”です。
私たちが手に入れられるデータは、多くの場合「母集団の一部(標本)」だけです。
つまり、
- 考え得るすべての対象者の平均ではなく、
- 研究で観察された値(標本平均の差)
をもとに分析している、ということです。
例えば心不全の薬の効果の研究であれば、知りたいのは全ての心不全患者さんの平均的投薬効果です。しかし、現実にはすべての患者さんのデータは手に入りません。勤め先などでデータを取れる患者さんで研究する事になります。この時入手できたデータは、知りたい集団(全ての心不全患者)の特性とぴったり合っているとは限りません。
そのため、ほとんどの研究は入手できたデータから、平均値や効果量などを知りたい集団全体の推定値として計算しています。
点推定と区間推定
統計的な推定には主に2種類あります:
| 推定方法 | 内容 |
| 点推定 | 「この1点が真の値だ」と考える |
| 区間推定 | 「この範囲ならだいたい真の値を捉えているだろう」と考える |
信頼区間は、後者の「区間推定」にあたります。
95%信頼区間とは?
95%信頼区間とは、
「この範囲内に、95%の確率で“真の値”が含まれているだろう」
という推定のことです。
つまり、研究を100回繰り返せば、約95回はこの信頼区間の中に真の値が含まれるという考え方になります。
例えば:
平均の差:3.2
95%信頼区間:[1.0, 5.4]
この場合、「差は3.2と推定されるが、真の差は1.0〜5.4のどこかにある可能性が高い」と読み取ります。
信頼区間は「統計の確からしさ」を可視化する
- 点推定だけだと、推定値の“信頼度”がわからない
- 信頼区間が狭ければ推定が安定しており、広ければ不確実性が高い
- p値だけでなく、信頼区間も一緒に見ることで、より実用的な解釈が可能になります
まとめ
| 用語 | 意味 |
| t検定 | 2群の平均の差が偶然か意味のあるものかを調べる手法 |
| p値 | 「差がなかったとして、偶然にこれだけの差が出る確率」 |
| 有意差 | 統計的に意味のある差があること |
| 自由度 | t分布の形を決める要素で、検定結果(p値)にも影響。効果量の計算に使う事もある。 |
| 効果量 | 差の大きさを示す指標(ばらつきに対する平均の差) |
統計の具体的なやり方を知りたい方へ
最後までお読みいただきありがとうございました
本ブログでは、JASPを使ったさまざまな統計手法のやり方をまとめています。初心者向けに手法別でわかりやすく解説していますので、ぜひこちらもご覧ください。
👉 JASPの統計手法まとめ記事を見る




コメント