統計検定のサンプルサイズって小さいとダメなの？
「サンプルサイズが小さいと検出力が下がる」
いろいろな書籍やネット上の記事で見かける内容です。
ふと、「サンプル数が程度小さいと、どの程度検出力が下がるのか」と疑問を持ったのですが、正直全然分かりません。
そこで、Rを使ってサンプルサイズと検出力の関係を調べてみました。
対象としたのは、独立2群のt検定で効果量d = 1.0、両側検定、有意水準0.05）という条件です。
サンプルサイズは、各群2〜30名まで段階的に変化させて、検出力を確認しました。
使用したRのコード
使用したRのコードは以下のものです。
library(pwr)
# 変数の定義
numbers <-c(2:30)
result <- c()
# 検出力を計算する関数の定義
cal_power <- function(n){
power_t_test <-pwr.t.test(d = 1.0,n = n,sig.level = 0.05,alternative = "two.sided",type = "two.sample")
return(power_t_test$power)
}
# 順次サンプル数を変更しながら、検出力を計算しリストに格納
for (i in numbers){
x <- cal_power(i)
result <- append(result,x)
}
# グラフ表示
plot(result,type = "o",xlab = "サンプル数",ylab = "検出力")
結果：検出力は結構下がる
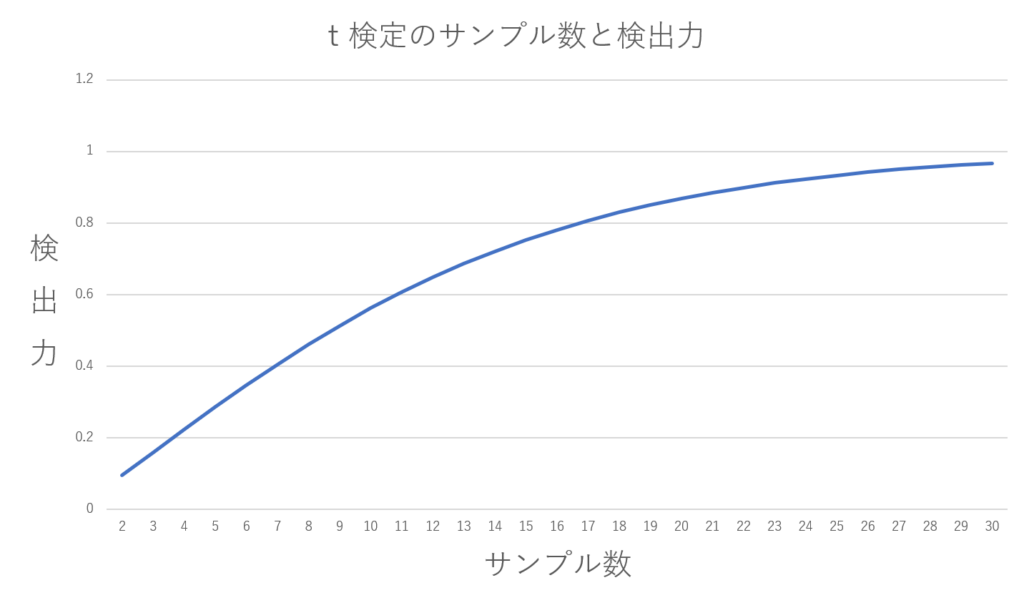
思っていたよりも検定力が低いことが分かりました。
効果量を1.0という比較的大きな値に設定しても、サンプルサイズが少ないと検出力はかなり低くなります。
たとえば：
- n = 5（5名 vs 5名） → 検出力は 約0.29
- n = 10 → 約0.56
- n = 15 → 約0.75
- n = 20 → 約0.87
感覚的には「効果量が大きければ、少ない人数でも検出できそう」と思っていましたが、現実はそう甘くないようです。特にn = 5や10のような小規模な研究では、「本当に差があっても見つからない」可能性が高くなることがわかりました。
リハビリや医療系の研究では、パイロットスタディとして10人前後の小規模サンプルの研究も見かけます。もちろん、探索的な研究や初期検討として大切な役割を果たしていると思います。
ただ、こうした結果を読むときは、「検出力が低いために差が見つからなかった」可能性も考慮すべきだと感じました。
結論：サンプル数が少ないのはやっぱり辛い
やっぱり小サンプルは厳しい。環境が許せばサンプルは各群20ぐらいは欲しいところ、というのが今回の感想です。今後何か検証する時や、文献を読む時の参考になれば幸いです。
思っていたより小サンプルの影響は強いようでした。個人的には意外性があったので、相関分析でもやってみる事にしました。次の記事ではピアソンの相関分析での検出力について検証しています。サンプルサイズと検出力の関係・相関係数の散らばり具合についてグラフも交えて紹介しています。
興味のある方は相関分析とサンプルサイズの記事も見てみてください。
コメント