はじめに
前回の記事では、「多重共線性とは何か？」「なぜ問題になるのか？」という点を、図や散布図を用いて直感的に解説しました。
今回はその続編として、「多重共線性の対処法」をテーマにお話しします。
多重共線性は、分析の目的や状況によって取るべき対策が異なります。そこでこの記事では、回避手法の特徴と使いどころを整理し、「どんなときに、どの手法を選べばよいのか？」を具体的に紹介していきます。
多重共線性（multicollinearity）とは？直感的な理解とチェック方法
「多重共線性とは わかりやすく」と検索されることが多いように、この概念はやや取っつきにくいものです。
簡単に言えば、説明変数（独立変数）同士に強い相関がある状態のことです。たとえば、「身長」と「足の長さ」は高い相関を持つため、同時に回帰モデルに入れると片方の影響がうまく分離できず、回帰係数が不安定になります。
こうした状況では、以下のような指標が役立ちます：
| 指標 | 説明 |
| 相関係数 | 2つの変数間のペア相関（±0.7以上は要注意） |
| VIF | Variance Inflation Factor（分散拡大要因）：他の変数との相関を考慮した“多変量の相関”指標。10以上は危険域とされることが多い |
ペア相関だけでは不十分
たとえば、どのペアでもそれほど相関が高くないのに、全体としては多重共線性が強いということもあります。このような場合、VIFのような多変量的な相関の指標を使う必要があります。
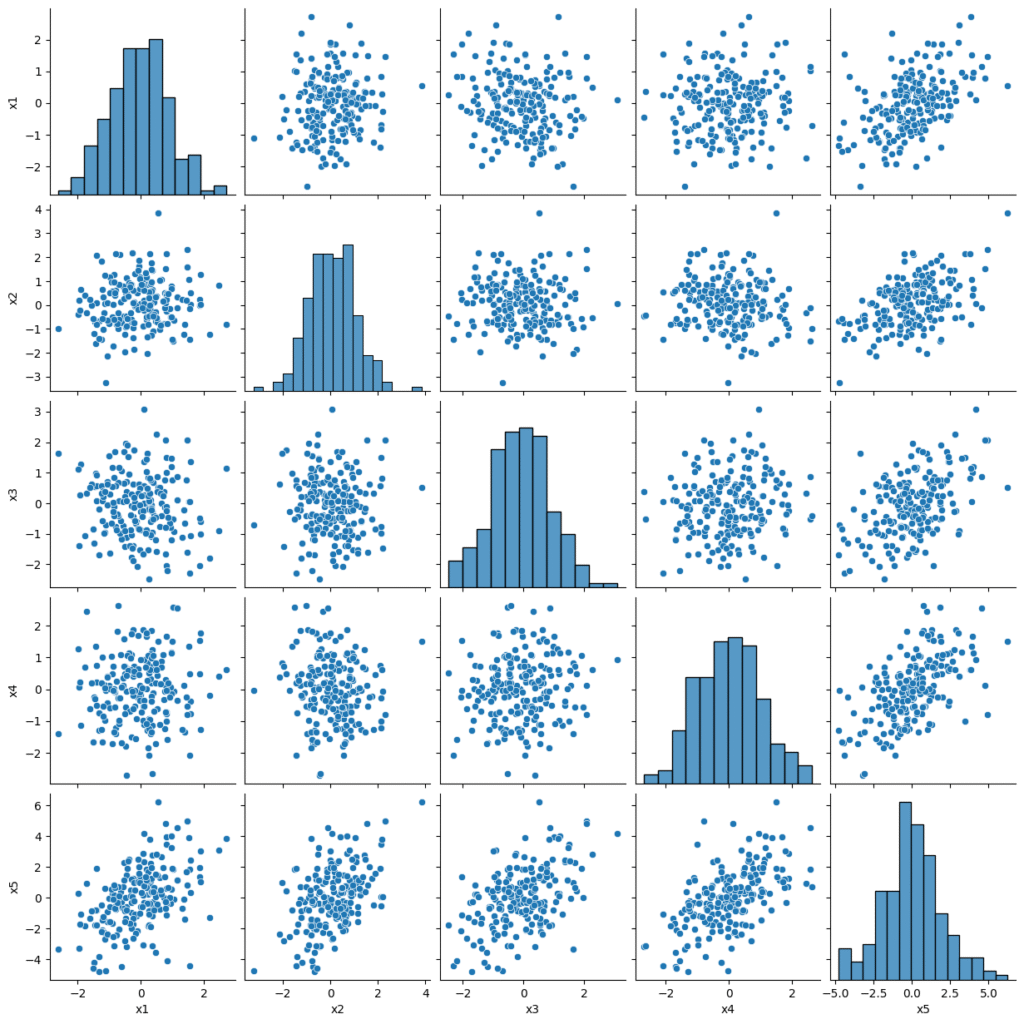
例えば変数X1～5とそれから導き出される変数Yがあるとします。この時に、X5がX1～4の合計に近い場合は、個別の相関係数が高くなくても多重共線性が強まります。
下のグラフでは一番下の行であるX5が、他の四つのデータの和になっています。それぞれの相関係数は0.4～0.5程度ですが、VIFを計算すると112という極めて高い数値が算出されます。このような相関構造を持つデータを扱う場合は、個別の相関係数チェックだけでは不十分です。
多重共線性の原因と起きやすい場面
多重共線性は、以下のような状況でよく発生します。
- 似たような意味を持つ変数を複数使っている（例：身長・体重・BMI）
- ダミー変数を過剰に生成した（カテゴリ変数のダミー化で1列落とし忘れた等）
- センサーデータや時系列データなど、変数間に自然と相関が生まれる構造のデータ
- サンプル数に対して変数数が多すぎる
回避策の選び方は「目的次第」
多重共線性の対処法は一つではありません。重要なのは、分析の目的に応じて対処法を選ぶことです。
| 目的 | 例 | 向いている手法 |
| 高精度な予測がしたい | 売上や仕入れの予測 | ランダムフォレスト、LightGBM、リッジ回帰 |
| 変数の意味を重視したい | 政策決定、経済分析など | VIFによる変数選択 |
| ドメイン知識を反映させたい | 医療や教育などの専門領域 | VIF、変数選択、リッジ回帰 |
| サンプル数が少ない | パイロットテストなど | リッジ回帰、主成分分析（PCA） |
各手法の特徴と使いどころ
主成分分析（PCA）
主成分分析は、相関の強い複数の変数をまとめて、新しい変数（主成分）に変換する方法です。これは「似た情報をひとつに集約する」イメージで、変数同士の重なりを減らし、多重共線性を解消します。
たとえば、身長・体重・BMIのように関連性が高い項目を、一つの“体格指標”に置き換えることで、モデルの安定性が向上します。
ただし、主成分は元の変数の意味をそのまま持たないため、解釈が難しくなるという欠点があります。
特徴
- 高次元（項目数の多い）・相関の強いデータに有効
- 変数間の関係を整理し、モデルの安定性を向上させる
- ただし、新しい変数の意味は直感的に分かりにくい
向いているケース
- 変数が多すぎて分析が複雑なとき
- 説明よりも予測精度を重視したいとき
リッジ回帰（Ridge回帰）
リッジ回帰は、回帰モデルの係数が大きくなりすぎないように制御する（L2正則化）手法です。多重共線性があると、回帰係数が不安定になり、小さなデータの変化で大きく変動してしまいます。
リッジ回帰はすべての変数を残しながら、係数を全体的に小さく抑えることで安定性を確保します。これにより、予測精度や汎用性が高まります。
特徴
- 変数を削除せずにモデルを安定化できる
- 多重共線性の影響を軽減
- データ数が少ない場合にも有効
- 機械的に調整されるため、解釈上重要な変数がモデルで重視されなくなることもある。
向いているケース
- 変数の意味を残したまま安定性を向上させたいとき
- サンプル数が少ないが変数が多いとき
ラッソ回帰（Lasso回帰）
ラッソ回帰は、不要な変数の係数を自動的にゼロにする（L1正則化）手法です。
これにより、重要な変数だけが残り、モデルをシンプルにできます。
多重共線性がある場合、似た変数のうちどれか一つを残して他をゼロにすることもあります。ただし、変数選択がデータに依存するため、選ばれる変数が変化してしまう場合があります。
特徴
- 変数選択と回帰を同時に行える
- モデルが簡潔になり解釈しやすい
- ただし、選択結果がデータによって不安定になることもある
- 機械的に調整されるため、解釈上重要な変数の影響を０にされてしまう事もあり得る。
向いているケース
- 変数が多く、どれが重要かを特定したいとき
- モデルをできるだけシンプルに保ちたいとき
VIF（Variance Inflation Factor）と専門知識による変数選択
VIFは、ある変数が他の変数とどの程度相関しているかを数値化する指標です。複数の変数が絡んだ複雑な相関構造があっても、それを検出できます。
多重共線性が強い場合、その変数のVIF値は高くなります。一般的には、VIFが10を超えると多重共線性の影響が大きいと判断されます。前回の記事の検証でもVIFが5を超えると明らかに精度が下がり、VIFが10を超えると精度は元の1/3～1/6程度になっていました。
VIFを使った変数選択では、VIFが高い変数を順に削除し、多重共線性を減らしてモデルを安定させます。
また、モデルを使用する領域の専門知識も併用して、変数の取捨選択を行います。ある変数のVIFが高くても臨床的に重要な意味を持つ可能性もあるため、統計的判断だけでなく、専門知識との併用により変数を選択していきます。
特徴
- 多重共線性を数値で明確に評価し、影響が強い変数を計画的に除外できる
- 変数削除により解釈性が向上する
- モデルを使用する分野の背景知識を使用して、合理的なモデルを作りやすい。
- 人間が変数を個別にみるため、手間がかかる。
向いているケース
- 変数の意味を重視したい
- モデルの解釈性が強く求められる場合
決定木系モデル（Decision Tree, Random Forest, XGBoostなど）
決定木モデルは、データを条件分岐の形で分類・予測する手法です。
「もしAなら○○、そうでなければ△△」というルールを繰り返し作っていくことで、結果を予測します。
多重共線性には比較的強く、変数の重要度を算出できるのも特徴です。さらにランダムフォレストやXGBoostのようなアンサンブル手法では、多くの決定木を組み合わせて予測精度を高めます。
ただし、単純な決定木は過学習（訓練データに合わせすぎて新しいデータで精度が落ちる現象）が起こりやすいため、剪定やパラメータ調整が必要です。
特徴
- 多重共線性に強く、変数の重要度を出せる
- シンプルな決定木なら分岐ルールにより直感的な解釈が可能
- アンサンブル手法で高い予測精度が期待できる
- 適切な調整を行わないと過学習のリスクあり。
向いているケース
- 予測精度と変数の重要度評価を両立したいとき
- データ量が多い時
多重共線性を“放置”してもよいケースとは？
目的によっては無理に対処する必要がない
「多重共線性は絶対に避けなければならない」と思われがちですが、予測モデルにおいては必ずしも除去しなくても問題ないことがあります。特に、以下のような目的の違いによって方針が変わります。
| 観点 | 因果推論（Causal Inference） | 予測モデル（Prediction Model） |
| 目的 | 説明変数の係数から因果効果を推定 | 目的変数の予測精度を最大化 |
| 多重共線性の影響 | 係数の推定が不安定になり、信頼区間が広がる → 因果効果の推定が困難 | モデルの予測精度には必ずしも大きく影響しない |
| 対処の必要性 | 高い（特に係数の解釈が必要な場合） | 低い（精度が落ちないなら放置も可） |
| 典型的な対策 | – 高VIF変数を削除 – 主成分分析（説明性低下の覚悟あり） – 実験設計で変数間の独立性を担保 | – Ridge/Lassoで安定化 – 決定木系モデルの利用 |
| 解釈性の重要度 | 高い（係数＝因果効果の推定値） | 必ずしも高くない（ブラックボックスでも可） |
おわりに：万能な対処法はない。目的に応じて選ぼう
多重共線性は、統計モデリングや機械学習において避けて通れない問題です。
しかし、その対処法は目的によって大きく異なります。因果関係の分析をしたいのか、予測精度を上げたいのか、モデルの解釈性を重視したいのか…。これらの視点に応じて、適切なアプローチを選ぶことが重要です。
コメント