はじめに|p値だけでは「どれくらい効いたか」は分からない
医療・リハビリ分野の論文では、
- 「p < 0.05 だった」
- 「有意差があった」
という表現をよく目にします。
しかし p値は「差があるかどうか」しか教えてくれません。
その差がどれぐらいなのか?を判断するために使われる指標が 効果量(effect size) です。
この記事では、統計が苦手な医療従事者の方向けに、
- 効果量とは何か
- p値との違い
- 効果量の種類と使い分け
- 解釈するときの注意点
を 数式なし・図解前提 で解説します。
効果量とは何か?|「差の大きさ」を表す指標
ざっくり言うと、効果量とは
データのばらつき具合と比べて、差がどれくらい大きいか
を表す指標です。
p値との違い
- p値:
- 偶然とは言えない差か?の指標
- サンプルサイズの影響を強く受ける
- 効果量:
- 差の大きさの指標
例えば、
- サンプル数が多い研究 → わずかな差でも p < 0.05 になりやすい
- サンプル数が少ない研究 → 差が大きくても有意にならないことがある
このような場面で、
「実際どれくらい違うのか?」 を補足してくれるのが効果量です。
効果量は「ばらつき」を基準にしている
多くの効果量は、
- 「平均の差(見たい変化の大きさ)」
- 「標準偏差(データのばらつき・個人差)」 という2つの要素を使って計算されます。
手法によっては平均値や標準偏差を直接使わないものもありますが、**「データのばらつきに対して、どれくらい確かな変化(変動)があったのか」**を数値化するという考え方は、すべての効果量に共通しています。
そのため、
- 集団のばらつきが大きい → 効果量は小さくなりやすい
- ばらつきが小さい → 効果量は大きくなりやすい
という性質があります。
文字だけだとわかりにくいので、グラフを見ながら考えてみましょう。
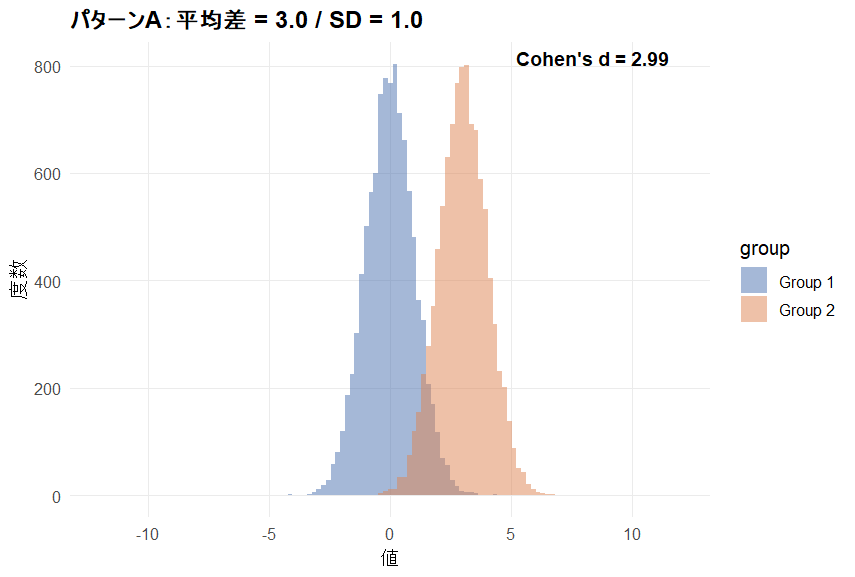
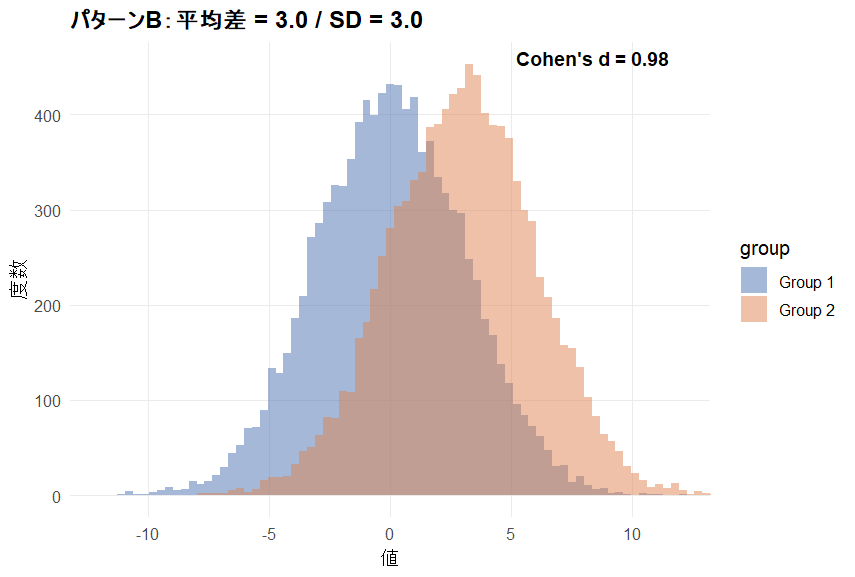
以下のパターンA/Bの2つのグラフはどちらも平均値の差が3.0の2群を比較したグラフです。
どちらも2群間の差は同じですが、データのばらつき具合に差があります。
効果量はばらつき具合をもとに計算されます。そのため平均値の差が同じでもデータのばらつきが違えば、効果量も違ってきます。
上のグラフではばらつきが小さい(SD = 1.0)ため、効果量がCohen`s d = 2.99と算出されています。
一方、下のグラフでは平均値の差は上と同様に3.0ですが、データのばらつき(SD = 3.0)も大きいため効果量はCohen`s d = 0.98と上のグラフより低く算出されています。
このように同党の変化があっても、元の集団のばらつき具合によって、効果量は大きく/または小さく算出されます。
※SDはばらつきの指標です。標準偏差とも言います。
他の論文と単純比較できない理由
効果量は その研究集団の特性に依存 します。
そのため、
- 対象者の重症度
- 測定誤差
- 評価尺度の特性
が大きく異なる研究同士を、
効果量だけで単純に比較するのは注意が必要 です。
ただし、対象集団や評価方法が非常に似ている場合には、介入効果を推定する参考になることもあります。
効果量の主な種類
統計検定の種類により、使用される効果量も違ってきます。
よく使用される効果量の一覧は以下の通りです。
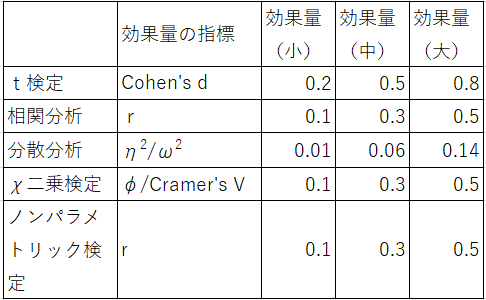
※参考 「水本 篤:効果量と検定力分析入門 ―統計的検定を正しく使うために― 2011」より一部改変。リンク先はJstageの該当ページです。
効果量の「小・中・大」は絶対ではない
よく目にする効果量の「小・中・大」の基準は、あくまでデータのばらつきに基づいた統計的な指標に過ぎません。その数値に「どれだけの価値があるか」は、別の視点で判断する必要があります。
「効果量」と「臨床的意義」は切り離して考える
統計的な効果量が小さくても臨床的に重要なケースもあれば、その逆も然りです。ここで重要になるのが、**MCID(最小臨床重要差)**という考え方です。
効果量: 統計的な「差のインパクト」
臨床的意義(MCID): 患者にとって「意味のある変化」か
例:下肢筋力1%の改善
同じ「1%の改善」でも、対象によってその価値は大きく変わります。
自宅退院を目指す高齢者: 1%の改善では生活動作に変化がなく、価値を感じにくいかもしれません。
アスリート: その1%が競技の勝敗を分ける決定的な差(MCID)になる可能性があります。
「効果量がある=臨床的に価値がある」と直結させず、常に「目の前の患者さんにとって意味がある差なのか?」を問い直すことが大切です。
サンプルサイズと効果量の関係
効果量には、p値のように「サンプルサイズが大きくなるほど、有意になりやすくなる(数値が変動する)」という性質はありません。しかし、サンプルサイズが小さいと推定の精度(信頼性)が不安定になるという点は共通しています。
具体的には、以下の要因に注意が必要です。
- 小規模研究のバラつき: サンプルサイズが小さいと、たまたま極端な結果が出たときに効果量が過大(あるいは過小)に評価されやすくなります。
- 信頼区間の幅: サンプルサイズが少ないほど信頼区間は広くなり、「真の効果量」がどこにあるのか確信が持てなくなります。
サンプル数と効果量の推定精度の関係をグラフで見てみましょう。
以下のグラフは、サンプルサイズと効果量の95%信頼区間の関係を例示したものです。
青線が推定された効果量の平均値で、水色の帯が効果量の95%信頼区間(推定精度)を示しています。帯の幅が狭いほうが推定精度が高い、という意味になります。
サンプルサイズが大きければ(グラフ右側)効果量の信頼区間も一定の範囲に収まりますが、サンプルサイズが25以下(グラフ左側)では精度が下がり、推定の幅が広がっているのが確認できます。
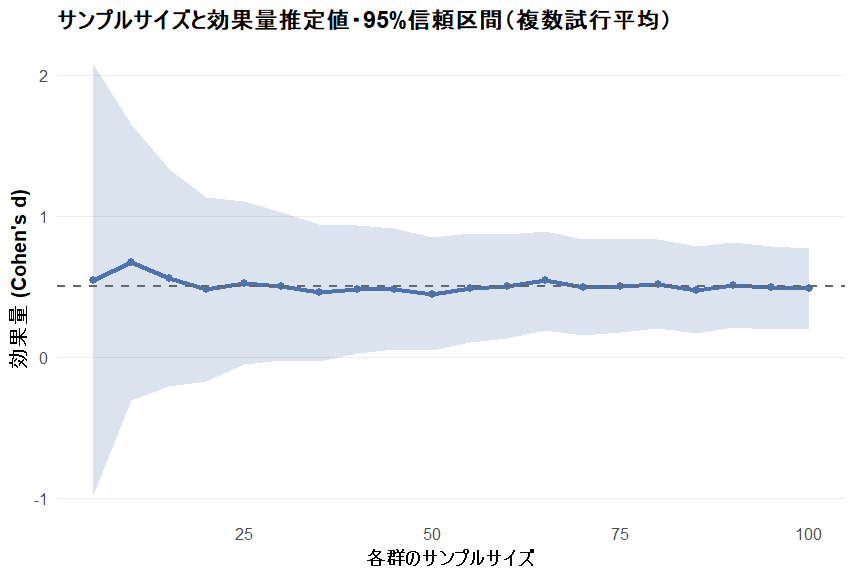
※プログラムにより生成された架空のデータをもとに作成しています。データは架空のものですが、サンプルサイズと信頼区間の関係については研究報告と同じ原理が働きます。
また、サンプルサイズが大きければ信頼区間は狭くなりますが、それでも「点推定値(一つの数値)」には常に不確実性が伴います。そのため、1件の小規模研究の結果や、効果量の平均値だけを見て判断するのは早計です。
論文に併記されていれば**「95%信頼区間(95%CI)」**も必ずセットで確認しましょう。具体的には、以下のように記載されるのが一般的です。
パターン1:信頼区間が「広い」場合
Cohen’s d = 0.8 (95% CI: 0.30 – 1.30)
効果量そのものは 0.8 と大きな値ですが、信頼区間の幅が 0.3 から 1.3 までと広く、推定値にバラつきがあります。これは、同じ実験を再度行った場合、結果が大きく変動する可能性があることを示唆しています。数値の見た目ほど「確かな結果」とは言えないため、解釈には慎重さが必要です。
パターン2:信頼区間が「狭い」場合
Cohen’s d = 0.4 (95% CI: 0.35 – 0.45)
一方、こちらの効果量は 0.4 と中程度ですが、信頼区間が 0.35 から 0.45 と非常に限定されています。何度実験を繰り返しても、効果はおよそ 0.4 前後に落ち着く可能性が高いと予想されます。つまり、こちらの結果の方が「見積もりの精度(信頼性)が高い」と判断できるのです。
どの効果量を見ればいいか迷ったら
初心者の方は、まず次を目安にすると十分です。
- t検定 → Cohen’s d
- 相関 → r
- 分散分析 → η²(可能なら ω²)
すべてを完璧に理解する必要はありません。
「p値+効果量を見る習慣」 が大切です。
まとめ|効果量は論文理解の解像度を上げる
- p値は「差があるか」を示す
- 効果量は「どれくらい違うか」を示す
- 効果量にも種類があり、統計手法ごとに異なる
- 数値の大小だけでなく、文脈と信頼区間が重要
効果量を意識することで、
「差があるのか?」
だけでなく、
「どれぐらいの差があるか?」
まで一歩踏み込んだ論文の読み方ができるようになります。




コメント