【初心者向け】クロスバリデーションとは？仕組み・目的・種類を図解！医療データの注意点も紹介

はじめに：モデル評価の「まぐれ」当たり
ホールドアウト法とは
クロスバリデーションとは
実験で見てみよう（LightGBMによる比較）
クロスバリデーションの種類
1. クロスバリデーションの種類（基本編）
2. クロスバリデーションの種類（応用編）
医療データでのポイント
医療データにおけるクロスバリデーションの落とし穴と注意点
まとめ

はじめに：モデル評価の「まぐれ」当たり

機械学習では、作ったモデルが「どのくらい正確に予測できるか」を評価する必要があります。
例えば、糖尿病の有無を予測するAIを作ったとします。学習したデータだけで良い結果が出ても、新しい患者で同じ精度が出るとは限りません。学習データでの予測精度よりも、新規データでの予測精度は下がるのが普通です。
→ この「一般化性能（汎化性能）」を確かめるのが「検証（validation）」の目的です。

たとえば、テストを受けた時の出題傾向によって、
「今回は昨日勉強した問題が出てうまくいった」
「今回は苦手な問題が出てしまった」
…というように結果が上下することがありますよね。

同じことが機械学習モデルにも起こります。
たまたま“得意なデータ”がテストに当たると高い精度が出ますが、“苦手なデータ”だと急に精度が下がることもあります。

しかし、業務や臨床で使用するAIモデルの評価がそんな「まぐれ」に左右されてしまっては困ります。ホールドアウト法と呼ばれるシンプルな評価方法では、条件により「まぐれ」が出やすくなります。
そこで登場するのがクロスバリデーションです。
クロスバリデーションは、こうした「偶然の当たり外れ（まぐれ判定）」を減らし、モデルの実力をより正確に測るための方法です。

ホールドアウト法とは

最もシンプルな検証方法です。
データを「学習用」と「テスト用」に分けて評価します。

例：80人のデータで学習し、20人でテストする（8:2分割）。

利点

計算が速く、手軽
一度の学習で済む

欠点

分け方によって結果が変わる（たまたま高齢者がテスト側に偏るなど）
データが少ないケースや不均衡データ※では、学習・テストの両方が不安定になる

医療の例

陽性患者が少ないデータセットで、たまたま陽性患者がテスト用データに偏ってしまった。その結果学習データに含まれる陽性患者が減って、予測精度が低くなってしまった。

※陽性症例が少ないデータを不均衡データと言います。

クロスバリデーションとは

データを複数のブロックに分割して検証する方法。
代表的なのが「k分割交差検証（k-fold cross validation）」です。一言で言うと、テストに使用するデータを変えながら何度も評価値を計算して平均を取る方法です。

分割数5（ｋ＝５）の場合の仕組み

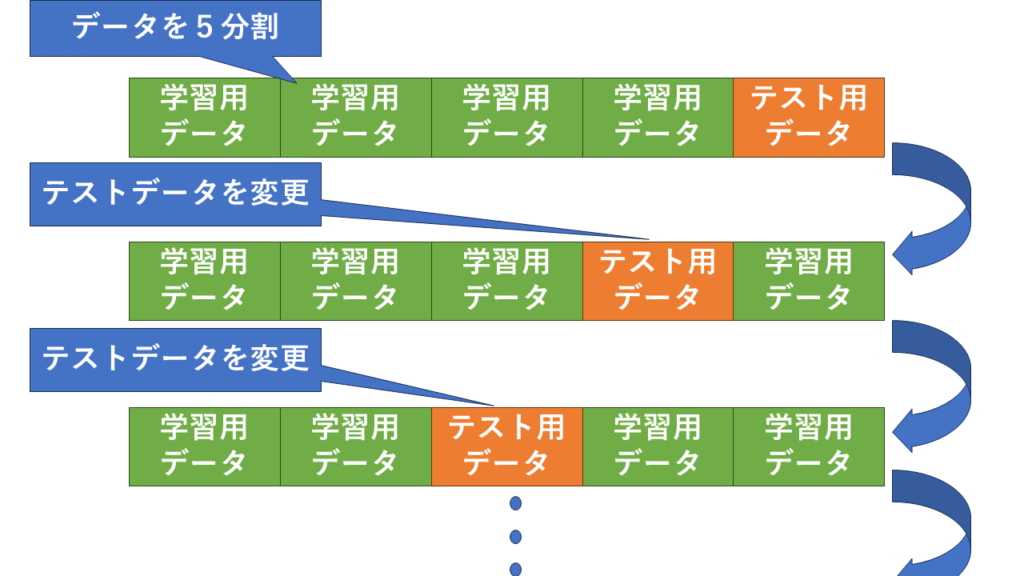
データを5個のグループ（fold）に分ける
そのうち1つをテスト用、残りを学習用にして学習
これをテスト用データを変えながら5回繰り返す
すべての結果の平均を取る

📈 メリット

データの分け方による偶然の影響を減らせる
小規模データでも安定した評価ができる
モデルの信頼性をより客観的に確認できる

⚙️ デメリット

計算コストが増える（モデルの学習と評価指標の計算を何度も行うため）

実験で見てみよう（LightGBMによる比較）

ここで、実際に LightGBM による予測モデルを用いて、
「ホールドアウト法」と「クロスバリデーション」でどのような違いが出るかを確認しました。

📊 実験条件

モデル：LightGBM（デフォルト設定）
繰り返し回数：40回（モデルの作成・学習と検証を40回実施）
比較方法：ホールドアウト法 vs 5分割クロスバリデーション（k=5）

🔹 回帰タスク（カリフォルニア住宅価格データ）

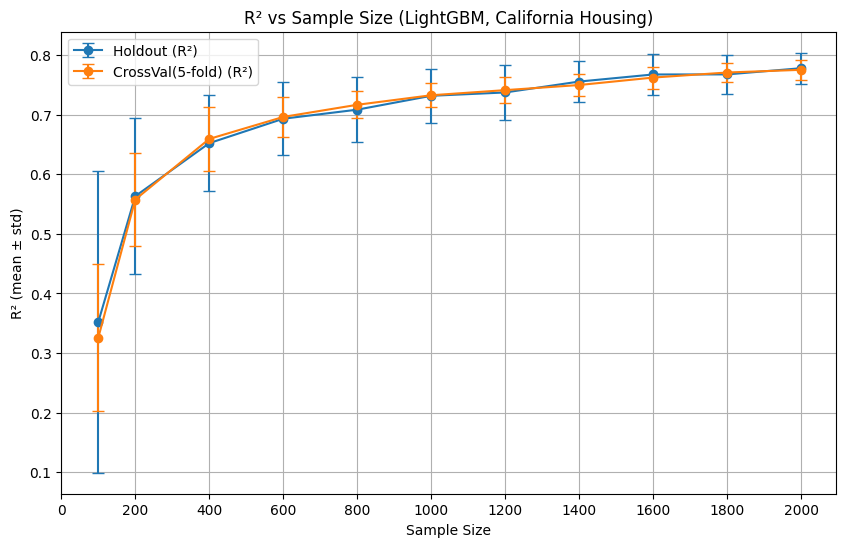
各サンプル数ごとにホールドアウト法（青）とクロスバリデーション（オレンジ）で
決定係数 R2 を算出しました。
それぞれの手順を40回繰り返し、平均値と標準偏差をグラフ化しています。折れ線グラフが平均値を示しており、縦の棒は試行ごとの検証結果のブレ幅を示しています。縦棒が長ければ、試行ごとにモデルの評価がバラついている事を示します。

※決定係数は回帰モデルの予測精度の指標で、数値が大きいほど良いモデルです。

結果の傾向：

サンプル数が少ないほど、ホールドアウト法（青）のばらつき（縦棒）が大きい。サンプル数が100程度だと、標準偏差がR2＝0.1（モデルがほとんど役に立たない）から、R2＝0.6（モデルがいくらか予測を当てている）という結果までブレ幅が非常に大きい。このレベルだと、R2が記載されていてもそれを鵜呑みにする事は出来ない。
クロスバリデーションの方が安定している。今回の実験の設定では評価のブレ幅はホールドアウト法の半分程度。
サンプル数が増えると、両者の差は小さくなる

分類タスク（糖尿病データ：Pima Indians Diabetes）

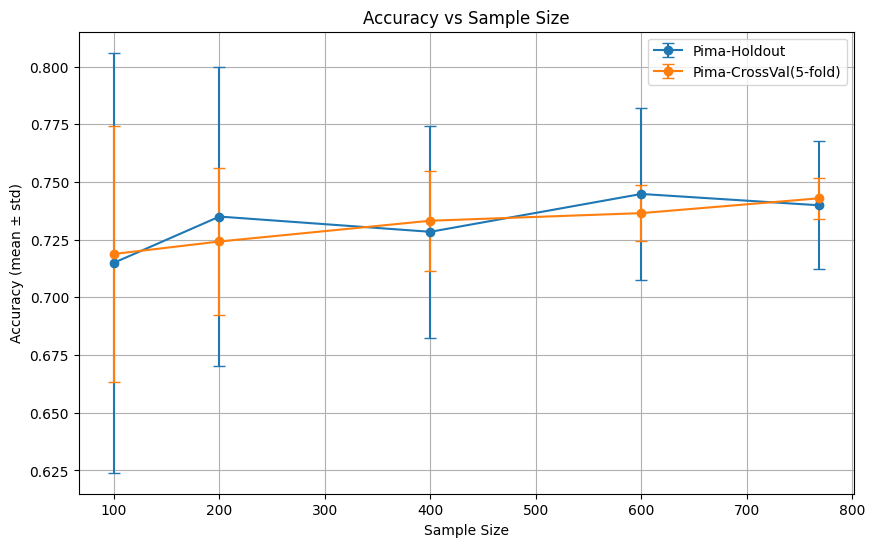
同様に、各サンプル数ごとにAccuracy（正解率）を40回測定し、平均値と標準偏差を算出しました。
この実験で使用したデータは、陽性データが30％ほどの軽度の不均衡データです。分割の際に陽性率を保つための層別化（stratified K-Fold）はしていません。

※Accuracyは分類モデルの予測精度の指標で、数値が大きいほど良いモデルです。

📊 結果の傾向：

ホールドアウト法（青）は分割の影響で評価指標の平均値も乱高下している。
クロスバリデーション（オレンジ）は精度のばらつきが小さく、サンプル数に応じて精度が徐々に上がっている。
データ数が増えるにつれて両者の差は縮まる

クロスバリデーションの種類

クロスバリデーションの種類（基本編）

種類	説明	用途
k分割法	一般的な方法。k=5や10が多い。	標準的な検証
LOOCV（Leave-One-Out）	1件をテストにして繰り返す。	データが極端に少ない場合
Stratified K-Fold	陽性・陰性の割合を保つように分割	医療データなど不均衡データに適している
Repeated K-Fold	分割を何度も繰り返す	安定した平均を得たいとき

※ 今回の実験では Repeated K-Fold（繰り返し付き交差検証）を用いています。

クロスバリデーションの種類（応用編）

ここまで紹介したk分割法や層化k分割法のほかにも、データの性質に合わせた応用的な手法があります。
とくに医療や時系列データでは、分割の仕方を誤るとモデル評価が過大に出てしまうことがあります。

種類	概要	典型的な用途
Group K-Fold	同じ患者や同じ施設など「グループ単位」で複数データがある場合、グループが学習用とテスト用に重ならないように分割します。	被験者ごとの複数検査データ、病院単位の記録など
Time Series Split（時系列CV）	データの時系列順を保ったまま、過去データで学習し未来データで検証します。	バイタルサイン、リハビリ経過、薬剤投与効果など時間依存データ

これらの方法は、特定の性質をもつデータ（グループ構造や時系列構造）で「データリーク（情報漏洩）」を防ぎ、より現実的な評価を行うために有効です。

医療データでのポイント

医療データはサンプル数が限られていることが多く、偏りが生じやすい。
だからこそ、一度の分割に依存しない評価（クロスバリデーション）が重要です。

さらに、疾患の有病率が低い場合は、層化（Stratified）クロスバリデーションを使うと良いです。

疾患の有病率が低いデータでは、精度評価の信頼性がより重要になります。データの分割によりたまたま陽性症例が学習データにあまり含まれなければ、モデルの学習にネガティブな影響が強く出てしまうでしょう。

医療データにおけるクロスバリデーションの落とし穴と注意点

医療データでは、**「情報リーク」**が最も起こりやすい落とし穴です。
同一患者の複数検査データが学習と検証の両方に混ざると、実際には「同じ人を当てている」ことになり、精度が過大に見積もられます。
こうした場合は、患者単位でデータを分ける Group K-Fold が推奨されます。
また、時間の経過を伴うデータでは、未来の情報を誤って学習してしまわないよう、Time Series Split を用いるのが安全です。

実際、私の職場でも機械学習モデルについて相談を受ける中で、そういったケースがありました。
ある回帰モデルで患者データをランダムに分割したところ、非常に高い精度（R² ≈ 0.95）が得られましたが、よく確認すると同じ患者の異なる検査データが学習と検証の両方に入っていました。
患者単位で分割し直すと精度は大幅に下がり（R² ≈ 0.65）、ようやく「現実的な性能」であることがわかりました。

この経験から、分割方法の設計こそが最も重要な検証工程だと痛感しました。

クロスバリデーションは強力な手法ですが、使い方を誤ると「正しい評価」ができません。機械学習モデルの作成では、以下のような設定ミスがしばしば生じます。